Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-30T19:37:08.932Z Has data issue: false hasContentIssue false
  • English
  • Français

On certain expansions of the solutions of the general Lamé equation

Published online by Cambridge University Press:  24 October 2008

A. Erdélyi
A. Erdélyi
Affiliation:
Mathematical InstituteThe UniversityEdinburgh 1
Get access Rights & Permissions [Opens in a new window]

Extract

1. In this paper I shall deal with the solutions of the Lamé equation

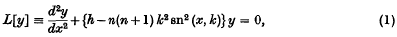
when n and h are arbitrary complex or real parameters and k is any number in the complex plane cut along the real axis from 1 to ∞ and from −1 to −∞. Since the coefficients of (1) are periodic functions of am(x, k), we conclude ](5), § 19·4] that there is a solution of (1), y0(x), which has a trigonometric expansion of the form

where θ is a certain constant, the characteristic exponent, which depends on h, k and n. Unless θ is an integer, y0(x) and y0(−x) are two distinct solutions of the Lamé equation.

It is easy to obtain the system of recurrence relations

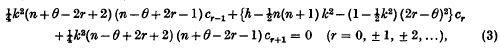
for the coefficients cr. θ is determined, mod 1, by the condition that this system of recurrence relations should have a solution {cr} for which

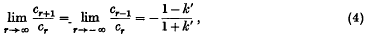
k′ being the principal value of (1−k2)½

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 38 , Issue 4 , November 1942 , pp. 364 - 367
Copyright
Copyright © Cambridge Philosophical Society 1942

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Erdélyi, A.On certain expansions of the solutions of Mathieu's differential equation. Proc. Cambridge Phil. Soc. 38 (1942), 28–33.CrossRefGoogle Scholar
(2)Erdélyi, A.Note on Heine's integral representation of associated Legendre functions. Phil. Mag. (7), 32 (1941), 351–2.CrossRefGoogle Scholar
(3)Hobson, E. W.The theory of spherical and ellipsoidal harmonics (Cambridge, 1931).Google Scholar
(4)Ince, E. L.Further investigations into the periodic Lamé functions. Proc. Roy. Soc. Edinburgh, 60 (1940), 83–99.CrossRefGoogle Scholar
(5)Whittaker, E. T. and Watson, G. N.Modern analysis (Cambridge, 1927).Google Scholar