Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Conte, Alberto
1978.
Varieta' di Cohen-Macaulay.
Rendiconti del Seminario Matematico e Fisico di Milano,
Vol. 48,
Issue. 1,
p.
181.
Wilson, P. M. H.
1978.
The behaviour of the plurigenera of surfaces under algebraic smooth deformations.
Inventiones Mathematicae,
Vol. 47,
Issue. 3,
p.
289.
Piene, Ragni
1979.
Algebraic Geometry.
Vol. 732,
Issue. ,
p.
503.
Shinagawa, Mitsuo
1982.
Some results on the normalization and normal flatness.
Hiroshima Mathematical Journal,
Vol. 12,
Issue. 1,
Catanese, Fabrizio
1984.
Algebraic Geometry Bucharest 1982.
Vol. 1056,
Issue. ,
p.
68.
Aleksandrov, A. G.
1986.
Euler-homogeneous singularities and logarithmic differential forms.
Annals of Global Analysis and Geometry,
Vol. 4,
Issue. 2,
p.
225.
Pinkham, Henry C.
1986.
A Castelnuovo bound for smooth surfaces.
Inventiones Mathematicae,
Vol. 83,
Issue. 2,
p.
321.
Elias, Juan
2013.
On the last Hilbert–Samuel coefficient of isolated singularities.
Journal of Algebra,
Vol. 394,
Issue. ,
p.
285.
Battistella, Luca
and
Carocci, Francesca
2023.
A smooth compactification of the space of genus two curves in projective space: via logarithmic geometry and Gorenstein curves.
Geometry & Topology,
Vol. 27,
Issue. 3,
p.
1203.


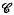 (denned in Section 1). If
(denned in Section 1). If 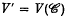 , to be closely connected with the normalization Ṽ.
, to be closely connected with the normalization Ṽ.