Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T13:49:36.835Z Has data issue: false hasContentIssue false
  • English
  • Français

On Banach algebra elements of thin numerical range

Published online by Cambridge University Press:  24 October 2008

R. R. Smith
R. R. Smith
Affiliation:
Texas A & M University, College Station, Texas 77843
Get access Rights & Permissions [Opens in a new window]

Extract

Among the elements of a complex unital Banach algebra 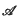the real subspace 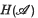of hermitian elements deserves special attention. This forms the natural generalization of the set of self-adjoint elements in a C*-algebra and exhibits many of the same properties. Two equivalent definitions may be given: 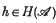if W(h) ⊂ 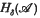, where W(h) denotes the numerical range of h (7), or if ║eiλh║ = 1 for all λ ∈ 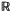. In this paper some related subsets 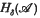are introduced and studied. For δ ≥ 0, an element 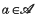is said to be a member of 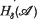if the condition

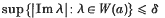
is satisfied. These may be termed the elements of thin numerical range if δ is small.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 86 , Issue 1 , July 1979 , pp. 71 - 83
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Alfsen, E. M.Compact convex sets and boundary integrals. Ergebnisse der Math. (Berlin, Springer, 1971).CrossRefGoogle Scholar
(2)Alfsen, E. M. and Effros, E. G.Structure in real Banach spaces I. Ann. of Math. 96 (1972), 98–128.CrossRefGoogle Scholar
(3)Alfsen, E. M. and Effros, E. G.Structure in real Banach spaces II. Ann. of Math. 96 (1972), 129–173.CrossRefGoogle Scholar
(4)Allen, G. D. and Ward, J. D.Hermitian liftings in B(lp). J. Operator Theory (in the Press).Google Scholar
(5)Andersen, T. B.Linear extensions, projections, and split faces. J. Functional Analysis 17 (1974), 161–173,CrossRefGoogle Scholar
(6)Asimow, L.Decomposable compact convex sets and peak sets for function spaces. Proc. Amer. Math. Soc. 25 (1970), 75–79.Google Scholar
(7)Bonsall, F. F. and Duncan, J.Numerical ranges of operators on normed spaces and of elements of normed algebras. (London Math. Soc. Lecture Note Series 2, Cambridge, 1971).CrossRefGoogle Scholar
(8)Bonsall, F. F. and Duncan, J.Numerical ranges II. (London Math. Soc. Lecture Note Series 10, Cambridge, 1972).Google Scholar
(9)Bonsall, F. F. and Duncan, J.Complete normed algebras (Berlin, Springer, 1973).CrossRefGoogle Scholar
(10)Chui, C. K., Smith, P. W., Smith, R. R. and Ward, J. D.L-ideals and numerical range preservation. Illinois J. Math. 21 (1977), 365–373.CrossRefGoogle Scholar
(11)Ellis, A. J.Some applications of convexity theory to Banach algebras. Math. Scand. 33 (1973), 23–30.CrossRefGoogle Scholar
(12)Sinclair, A. M.The states of a Banach algebra generate the dual. Proc. Edinburgh Math. Soc. 17 (1971), 341–344.CrossRefGoogle Scholar
(13)Sinclair, A. M.The norm of a hermitian element in a Banach algebra. Proc. Amer. Math. Soc. 28 (1971), 446–450.CrossRefGoogle Scholar
(14)Smith, R. R. and Ward, J. D.M-ideal structure in Banach algebras. J. Functional Analysis 27 (1978), 337–349.CrossRefGoogle Scholar
(15)Smith, R. R. and Ward, J. D.Applications of convexity and M-ideal theory to quotient Banach algebras. Quart. J. Math. (Oxford) (in the press).Google Scholar
(16)Smith, R. R.An addendum to ‘M-ideal structure in Banach algebras’. J. Functional Analysis (in the press).Google Scholar
(17)Tam, K. W.Isometries of certain function spaces. Pacific J. Math. 31 (1969), 233–246.CrossRefGoogle Scholar