Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-27T02:25:55.275Z Has data issue: false hasContentIssue false
  • English
  • Français

On Baker's inequality for linear forms in logarithms

Published online by Cambridge University Press:  24 October 2008

Alfred J. van der Poorten
Alfred J. van der Poorten
Affiliation:
University of New South Wales
Get access Rights & Permissions [Opens in a new window]

Abstract

Let α1, …, αn an be non-zero algebraic numbers with degrees at most d and heights respectively Al, …, An (all Aj ≥ 4) and let b1, …, bn be rational integers with absolute values at most B (≥ 4). Denote by p a prime ideal of the field 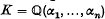and suppose that p divides the rational prime p. Write

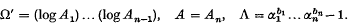
Then it is shown that

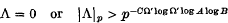
for some effectively computable constant C > 0 depending only on n, d and p. The argument suffices to prove similarly that in the complex case, if

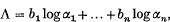
for any fixed determination of the logarithms, then

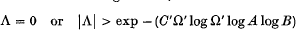
for some effectively computable constant C′ > 0 depending only on n and d (and he determination of the logarithms).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 80 , Issue 2 , September 1976 , pp. 233 - 248
Copyright
Copyright © Cambridge Philosophical Society 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Baker, A.Linear forms in the logarithms of algebraic numbers. IV. Mathematika 15 (1968), 204–216.CrossRefGoogle Scholar
(2)BAkER, A. and Stark, H. M.On a fundamental inequality in number theory. Ann. of Math. 94 (1971), 190–199.CrossRefGoogle Scholar
(3)Baker, A.A sharpening of the bounds for linear forms in logarithms. Acta Arith. 21 (1972), 117–129.CrossRefGoogle Scholar
(4)Baker, A. A central theorem in transcendence theory, in Osgood, C. F. ed. Diophantine approximation and its applications, pp. 1–23 (Academic Press, 1973).Google Scholar
(5)Baker, A.A sharpening of the bounds for linear forms in logarithms. III. Acta Arith. (1975).CrossRefGoogle Scholar
(6)Baker, A. and Coates, J.Fractional parts of powers of rationals. Math. Proc. Cambridge Philos. Soc. 77 (1975), 269–279.CrossRefGoogle Scholar
(7)Baker, A.Transcendental Number Theory (Cambridge University Press, 1975).CrossRefGoogle Scholar
(8)Coates, J.An effective p-adic analogue of a theorem of Thue. Acta Arith. 15 (1969), 279–305CrossRefGoogle Scholar
(9)Mahler, K.Über transzendente P-adische Zahlen. Compositio Math. 2 (1935), 259–275.Google Scholar
(10)Van Der Poorten, A. J.Hermite interpolation and p-adic exponential polynomials. J. Austral. Math. Soc. (to appear).Google Scholar
(11)Tijdeman, R.On the equation of Catalan. Acta Arith. 29 (1976), 197–209.CrossRefGoogle Scholar