Published online by Cambridge University Press: 24 October 2008
The differential analyser has been used to evaluate solutions of the equation
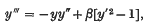
with boundary conditions y = y′ = 0 at x = 0, y′ → 1 as x → ∞, which occurs in Falkner and Skan's approximate treatment of the laminar boundary layer. A numerical iterative method has been used to improve the accuracy of the solutions, and the results show that the accuracy of the machine solutions is about 1 in 1000, or rather better.
It is shown that the conditions are insufficient to specify a unique solution for negative values of β a discussion of this situation is given, and it is shown that for the application to be made of the solution the appropriate condition is that y′ → 1 from below, and as rapidly as possible, as x → ∞. The condition that y′ → 1 from below can be satisfied only for values of β0, greater than a limiting value β0, whose value is approximately − 0·199, and which is related to the point at which the laminar boundary layer breaks away from the boundary.
* Falkner, V. M. and MissSkan, S. W., Phil. Mag. 12 (1931), 865;CrossRefGoogle ScholarAero. Res. Comm. R. and M. 1314.Google Scholar
† Bush, V., J. Franklin Inst. 212 (1931), 447.CrossRefGoogle Scholar
‡ Hartree, D. R., Nature, 135 (1935), 940.CrossRefGoogle Scholar
§ Falkner and Skan, loc. cit. equation (11).
* Falkner and Skan, loc. cit. equation (26).
* It is assumed here that Δy does not increase so rapidly that y″ Δy does not tend to zero; this is confirmed by the solution (11), since there is an exponential factor in the asymptotic approach of y″ to 0, and Δy only increases as a power of x.
† Whittaker, and Watson, , Modern Analysis (4th ed.) (Cambridge, 1927),Google Scholar § 16·5.
* This argument assumes that if Δ1y′ is the variation of y′ for a change Δβ of β, then Δ1y′/Δβ does not tend to zero as rapidly as y″, which is found to be the case.
* V. Bush, loc. cit.
† Loc. cit. Table I. Their results extend to β = 4/3 only. y″(0) of the present paper is −2a 2/[F 2(s)]½ in Falkner and Skan's notation.
* The counters are of the “direct drive” type, reading to tenths of a revolution, and the number of revolutions of the y′ counter was 1024y′, so that the last figure of the counter reading corresponds to a fourth decimal in y′. This fourth decimal was kept in the readings and interpolations, though it was expected that it would be purely nominal.
* Howarth, L., Aero. Res. Comm. R. and M. 1632 (1934), p. 10,Google Scholar equation (2·43), pp. 11, 12, and Table I.
† Falkner, V. M., Phil. Mag. 21 (1936), 624.CrossRefGoogle Scholar