Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-29T22:29:02.359Z Has data issue: false hasContentIssue false
  • English
  • Français

On a separation theorem of Rogers

Published online by Cambridge University Press:  24 October 2008

Roy O. Davies
Roy O. Davies
Affiliation:
University of Leicester and Purdue University
Get access Rights & Permissions [Opens in a new window]

Extract

In (1) (where references and terminology may be found), C. A. Rogers has proved the following surprising theorem.

Let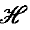be a class of sets, all Souslin-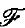in a topological space X. If A is a Souslin-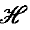set and B is an analytic set that does not meet A, then there is a Borelian-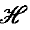set C with A ⊂ C and C ∩ B = Ø

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 75 , Issue 3 , May 1974 , pp. 357 - 359
Copyright
Copyright © Cambridge Philosophical Society 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Rogers, C. A.Lusin's first separation theorem. J. London Math. Soc. (2) 3 (1971), 103–108.CrossRefGoogle Scholar
(2)Sierpiński, W.Le théorème de M. Souslin dans la théorie des ensembles. Fund. Math. 25 (1935), 29–32.CrossRefGoogle Scholar
(3)Sierpiński, W.Algèbre des ensembles (Warsaw, 1951), pp. 190–192.Google Scholar