On a new analytical representation of curves in space
Published online by Cambridge University Press: 24 October 2008
Extract
It was in a paper bearing this title that Cayley(1) first considered the problem of representing a curve in projective space of three dimensions by means of the complex of lines which meet the curve. He took the conic given by the equations
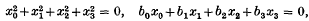
and found that the line
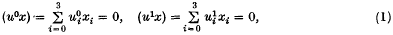
with dual Grassmann coordinates (…,pij,…), where
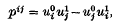
intersects the conic if, and only if,
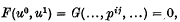
where F(u0, u1) is homogeneous and of degree 2 in both sets of indeterminates u0 and u1 and G(…,pij,…) is a form of degree 2 in the pij. Both F(u0, u1) and G(…,pij,…) are easily determined in this case.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 43 , Issue 4 , October 1947 , pp. 455 - 458
- Copyright
- Copyright © Cambridge Philosophical Society 1947
References
- 2
- Cited by


