Solving a problem of Erdős(5), I recently proved (4) that for n = 1, 2, …, the hypothesis 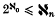implies that if the lines in the Euclidean space Ek (k ≥ 2) are distributed into n + 2 disjoint classes Li(i = 1, …,n + 2), then there exists a decomposition of Ek into 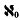sets Si such that the intersection of each line of Li with the corresponding set Si is finite. Without assuming any hypothesis other than the axiom of choice, I have also recently proved (3) that if di (i = 1,2,…) is any infinite sequence of mutually non-parallel lines in the plane, then the plane can be decomposed into N0 sets Si such that each line parallel to di intersects the corresponding set 8i in at most a single point.