Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-29T19:01:45.246Z Has data issue: false hasContentIssue false
  • English
  • Français

On a class of renewal functions

Published online by Cambridge University Press:  24 October 2008

D. J. Daley
D. J. Daley
Affiliation:
Statistical Laboratory, University of Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Renewal processes in discrete time (or as they are commonly termed, recurrent events) are appropriately described by renewal sequences {un} which are generated by discrete distributions 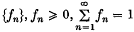, according to the equation

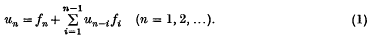
Any two renewal sequences {u′n}, {u″n} define another renewal sequence {un} by means of their term-by-term product {un} = {u′nu″n}, for the joint occurrence of two independent recurrent events ℰ′ and ℰ″ is also a recurrent event. Considering a renewal process in continuous time for which we shall suppose a frequency function f(x) of the lifetime distribution exists, so that a renewal density exists, the analogous property would be that for two renewal density functions h1(x) and h2(x), the function h(x) = h1(x) h2(x) is a renewal density function. A little intuitive reflexion shows that while h(x) dx has a probability density interpretation, this is not in general true of h1(x) h2(x) dx. It is not surprising therefore to find in example 1 a case where the product of two renewal densities is not a renewal density. Example 2, on the other hand, shows that in some cases it is true, and taken together with example 1, there is suggested the problem of characterizing the class of renewal densities h(x) for which αh(x) is a renewal density for all finite positive α and not merely α in 0 < α ≤ A < ∞. In turn this characterization enables us to define a class 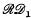of renewal densities for which h1(x) and 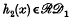imply that .

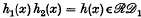Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 61 , Issue 2 , April 1965 , pp. 519 - 526
Copyright
Copyright © Cambridge Philosophical Society 1965

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bartlett, M. S.Recurrence and first passage times. Proc. Cambridge Philos. Soc. 49 (1953), 263–275.CrossRefGoogle Scholar
(2)Gnedenko, B. V. and Kolmogorov, A. N.Limit distributions for sums of independent random variables (translated by Chung, K. L.) (Addison–Wesley; Cambridge, Mass., 1954).Google Scholar
(3)Kingman, J. F. C.The stochastic theory of regenerative events. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete, 2 (1964), 180–224.CrossRefGoogle Scholar
(4)Kingman, J. F. C.On doubly stochastic Poisson processes. Proc. Cambridge Philos. Soc. 60 (1964), 923–930.Google Scholar
(5)Smith, W. L.Renewal theory and its ramifications. J. Roy. Statist. Soc. Ser. B, 20 (1958), 243–302.Google Scholar
(6)Smith, W. L. Infinitesimal renewal processes. In Contributions to probability and statistics (Stanford University Press, 1960).Google Scholar
(7)Widder, D. V.The Laplace transform (Princeton University Press, 1941).Google Scholar