Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-30T19:35:46.439Z Has data issue: false hasContentIssue false
  • English
  • Français

The nuclearity of operators generated by Hölder continuous kernels

Published online by Cambridge University Press:  24 October 2008

James Alan Cochran
James Alan Cochran
Affiliation:
Department of Mathematics Virginia Polytechnic Institute and State University Blacksburg, Virginia 24061
Get access Rights & Permissions [Opens in a new window]

Extract

Introduction. The space Cp is the class of operators on a Hilbert space for which the norm ∥K∥p = [trace (KK*)P/2]/p is finite. Equivalently, a compact operator is in Cp if

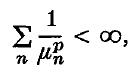
where the μn are the so-called ‘singular values’ of K (characteristic values of the non-negative compact operator [K] ≡ (KK*)½). The case p = 2 gives the familiar class of Hilbert–Schmidt operators, while C1 is the collection of trace-class or nuclear operators considered by Schatten(12), Lidskii(11), and Gohberg and Krein(7), among others.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 75 , Issue 3 , May 1974 , pp. 351 - 356
Copyright
Copyright © Cambridge Philosophical Society 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Chang, S. H.A generalization of a theorem of Lalesco. J. London Math. Soc. 22 (1947), 185–189.CrossRefGoogle Scholar
(2)Chang, S. H.On the distribution of the characteristic values and singular values of linear integral equations. Trans. Amer. Math. Soc. 67 (1949), 351–367.CrossRefGoogle Scholar
(3)Chang, S. H.A generalization of a theorem of Hille and Tamarkin with applications. Proc. London Math. Soc. (3) 2 (1952), 22–29.CrossRefGoogle Scholar
(4)Cochran, J. A.The existence of eigenvalues for the integral equations of laser theory. Bell System Tech. J. 44 (1965), 77–88.CrossRefGoogle Scholar
(5)Cochran, J. A.The analysis of linear integral equations. New York: McGraw-Hill, 1972.Google Scholar
(6)Fredholm, I.Sur une classe d'équations fonctionnelles. Acta Math. 27 (1903), 365–390; see also: Oeuvres Complètes. Malmö, 1955, 81–106.CrossRefGoogle Scholar
(7)Gohberg, I. C. and Krein, M. G.Introduction to the theory of linear non-selfadjoint operators. (Amer. Math. Soc. Translations of Math. Mono. 18.) 1969.Google Scholar
(8)Hardy, G. H. and Littlewood, J. E.A convergence criterion for Fourier series. Math. Z. 28 (1928), 612–634; see also: Collected Papers of G. H. Hardy, vol. III. Oxford: Clarendon Press 1969, 28–51.CrossRefGoogle Scholar
(9)Hardy, G. H. and Littlewood, J. E.Notes on the theory of series (IX): On the absolute convergence of Fourier series. J. London Math. Soc. 3 (1928), 250–253; see also: Collected Papers of G. H. Hardy, op. cit., 52–56.CrossRefGoogle Scholar
(10)Hille, E. and Tamarkin, J. D.On the characteristic values of linear integral equations. Acta Math. 57 (1931), 1–76.CrossRefGoogle Scholar
(11)Lidskii, V. B.Non-solfadjoint operators with trace. Doki. Akad. Nauk SSSR 125 (1959), 485–487; translated in Amer. Math. Soc. Transl. (2) 47 (1965), 43–46.Google Scholar
(12)Schatten, R.Norm ideals of completely continuous operators. Berlin: Springer-Verlag, 1960.CrossRefGoogle Scholar
(13)Smithies, F.The Eigen-values and singular values of integral equations. Proc. London Math. Soc. (2) 43 (1937), 255–279.Google Scholar
(14)Waraszkiewicz, Z.Remarque sur un théorème do M. Zygmund. Pol. Akad. Umiej. Krakow Wydz. Mat.-Przy. A., (1929), 275–279.Google Scholar
(15)Weidmann, J.Integraloperatoren der Spurkiasse. Math. Ann. 163 (1966), 340–345.CrossRefGoogle Scholar
(16)Zygmund, A.Remarque sur la convergence absolue des séries de Fourier. J. London Math. Soc. 3 (1928), 194–196.CrossRefGoogle Scholar