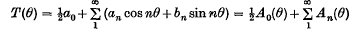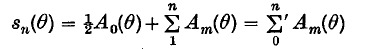Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Salem, R.
1949.
Convexity theorems.
Bulletin of the American Mathematical Society,
Vol. 55,
Issue. 9,
p.
851.
Sunouchi, Gen-ichirô
1951.
Notes on Fourier analysis (XXXIX).
Tohoku Mathematical Journal,
Vol. 3,
Issue. 1,
Watari, Chinami
1957.
On generalized Walsh Fourier series, I.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 33,
Issue. 8,
Watari, Chinami
1958.
On generalized Walsh Fourier series.
Tohoku Mathematical Journal,
Vol. 10,
Issue. 3,
Gosselin, Richard P.
1959.
Some theorems on 𝐿^{𝑝} Fourier series.
Transactions of the American Mathematical Society,
Vol. 92,
Issue. 2,
p.
291.
Yadav, B. S.
1967.
On the almost everywhere convergence of Fourier series.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 63,
Issue. 3,
p.
703.
Zygmund, A.
and
Fefferman, Robert
2003.
Trigonometric Series.