Note on the law that light-rays are the null geodesics of a gravitational field
Published online by Cambridge University Press: 24 October 2008
Extract
In the “special” or “restricted” theory of relativity, for which the line-element ds of the “world” of space-time is given by 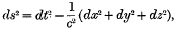 , the geodesics of the world are straight lines, and the null geodesics (i.e. the geodesics for which ds vanishes) are the tracks of rays of light. When Einstein discovered the “general“ theory of relativity, in which the effects of gravitation are taken into account, he carried over this principle by analogy, and asserted its truth for gravitational fields; it was, in fact, the basis of his famous calculation of the deviation of light at the sun. The law was, however, not proved at the time: and indeed there is the obvious difficulty in proving it, that strictly speaking there are no “rays” of light—that is, electromagnetic disturbances which are filiform, or drawn out like a thread—except in the limit when the frequency of the light is infinitely great: in all other cases, diffraction causes the “ray” to spread out over a three-dimensional region.
, the geodesics of the world are straight lines, and the null geodesics (i.e. the geodesics for which ds vanishes) are the tracks of rays of light. When Einstein discovered the “general“ theory of relativity, in which the effects of gravitation are taken into account, he carried over this principle by analogy, and asserted its truth for gravitational fields; it was, in fact, the basis of his famous calculation of the deviation of light at the sun. The law was, however, not proved at the time: and indeed there is the obvious difficulty in proving it, that strictly speaking there are no “rays” of light—that is, electromagnetic disturbances which are filiform, or drawn out like a thread—except in the limit when the frequency of the light is infinitely great: in all other cases, diffraction causes the “ray” to spread out over a three-dimensional region.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 24 , Issue 1 , January 1928 , pp. 32 - 34
- Copyright
- Copyright © Cambridge Philosophical Society 1928
References
* Phys. Zeits. XXI (1920), p. 659.Google Scholar
- 8
- Cited by


