In a paper recently published I found it necessary to extend those investigations of Lord Rayleigh which deal with the instability of the surface common to two streams of fluid. The Rayleigh investigation is equivalent to a first order approximation to the flow and concludes that the initial form of the disturbance of the common surface is maintained but that its amplitude increases exponentially with the time, the form of the surface at time t being, with particular values inserted,

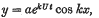
where a is the initial amplitude, 2π/k the wave-length, U the velocity of the upper stream, – U the velocity of the lower stream, and ρ the density of both fluids. A second order approximation to the flow for the above particular case shows that the original disturbance does not grow symmetrically, the ordinate of the common surface being given by

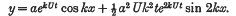
(A slightly amended form of this solution is given byequation III(8).) The solution suggests the initial stages in the formation of vortices. The problem was further discussed by a numerical step-by-step method and showed the formation of vortices quite clearly.