Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T14:15:08.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on the derivation of fluctuation formulae for statistical assemblies

Published online by Cambridge University Press:  24 October 2008

M. S. Bartlett
M. S. Bartlett
Affiliation:
Queens' College
Get access Rights & Permissions [Opens in a new window]

Extract

1. A familiar device in the study of statistical distributions is to form the moment-generating function

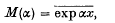
where the bar denotes averaging over all values of the statistical variate x. The moments μr of x are the coefficients of αr/r!, and the derived coefficients in the expansion of K ≡ log M are termed the semi-invariants kr. In particular,

and, for the normal (Gaussian) law,

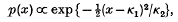
we have the simple formula

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 33 , Issue 3 , July 1937 , pp. 390 - 393
Copyright
Copyright © Cambridge Philosophical Society 1937

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Fowler, R. H.Statistical mechanics, 2nd ed. (Cambridge, 1936.)Google Scholar
(2)Wishart, J. and Bartlett, M. S.Proc. Camb. Phil. Soc. 29 (1933), 260–70.CrossRefGoogle Scholar