Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T11:23:42.039Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Some Integrals Involving Bessel Functions

Published online by Cambridge University Press:  24 October 2008

C. Fox
C. Fox
Affiliation:
Sidney Sussex College.
Get access Rights & Permissions [Opens in a new window]

Extract

The object of this note is to prove the following results, all of which hold when |a| < 1.

(2) If r is any positive integer other than zero, the

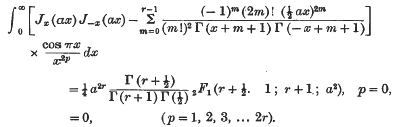
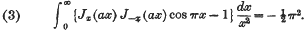
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 25 , Issue 2 , April 1929 , pp. 130 - 131
Copyright
Copyright © Cambridge Philosophical Society 1929

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Equations (1) and (3) were suggested for positive values of a(0<a<l) by some theorems of mine in null series (Proc. London Math. Soc. (2), 26 (1927), p. 54, Theorems 2 and 3). These theorems can be applied to transform Kapteyn series into integrals, but the proofs are very elaborate. For the proof below I am very much indebted to the referee. Apart from its simplicity it is true for complex values of a in the more extensive region |a| < 1.Google Scholar

† Watson, , Theory of Bessel Functions, p. 147 (5).Google Scholar

* Bromwich, , Theory of infinite series, 2nd Ed., p. 500, Theorem B.Google Scholar