Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T06:04:36.092Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on Ramanujan's arithmetical function τ (n)

Published online by Cambridge University Press:  24 October 2008

G. H. Hardy
G. H. Hardy
Affiliation:
Trinity College
Get access Rights & Permissions [Opens in a new window]

Extract

In his remarkable memoir ‘On certain arithmetical functions’* Ramanujan considers, among other functions of much interest, the. function τ(n) defined by

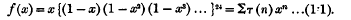
This function is important in the theory of the representation of a number as a sum of 24 squares. In fact

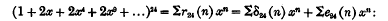
where r24 (n) is the number of representations;

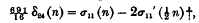
where σs(n) is the sum of the 8th powers of the divisors of n, and 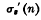the sum of those of its odd divisors; and

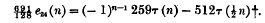
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 23 , Issue 6 , April 1927 , pp. 675 - 680
Copyright
Copyright © Cambridge Philosophical Society 1927

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Ramanujan, S., ‘On certain arithmetical functions’, Trans. Camb. Phil. Soc., 22 (1916), 159–184.Google Scholar

† Ramanujan, l.c., 179, 184. A function with argument ½n is zero when n is odd.

‡ Mordell, L. J., ‘On Mr Ramanujan“s empirical expansions of modular functions’, Proc. Camb. Phil. Soc., 19 (1920), 117–124 (a paper communicated in 1917).Google Scholar

* Ramanujan, l.c., 168, 171.

† That is to say τ(n)≠o(n5). See Ramanujan, l.c., 171.

‡ Ramanujan, l.c., 175.

* Hardy, G. H. and Littlewood, J. E., ‘Some problems of Diophantine approximation: II: The trigonometrical series associated with the elliptic theta-functions’, Acta Math., 37 (1914), 193–238.CrossRefGoogle Scholar

† 226 et seq.

* The function −6 log (1/λ) − 2πλ becomes negatively infinite when λ → 0 or λ → ∞, and has a maximum when πλ = 3. Here λ > ½.

* The maximnm of u αe −αy occurs for u = α/y, outside the range of integration because c > α.

† Fundamenta nova § 66.