Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-30T22:18:15.494Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on Ramanujan's arithmetical function τ(n)

Published online by Cambridge University Press:  24 October 2008

J. R. Wilton
J. R. Wilton
Affiliation:
Trinity College
Get access Rights & Permissions [Opens in a new window]

Extract

The function τ (n), defined by the equation

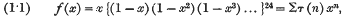
is considered by Ramanujan* in his memoir “On certain arithmetical functions”

The associated Diriċhlet series

converges when σ = > σ0, for a sufficiently large positive σ0.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 25 , Issue 2 , April 1929 , pp. 121 - 129
Copyright
Copyright © Cambridge Philosophical Society 1929

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Trans. Camb. Phil. Soc. 22 (1916), 159–184 (Collected papers, No. 18).Google Scholar

† Proc. Camb. Phil. Soc. 19 (1920), 117–124 (communicated 1917).Google Scholar

‡ Collected papers, 153–154.Google Scholar

§ Hardy, G. H., “Note on Ramanujan's arithmetical function τ(n)”, Proc. Camb. Phil. Soc. 23 (1927), 675–680.CrossRefGoogle Scholar

* Wigert, S., “Sur quelques functions arithmétiques”, Acta Math. 37 (1914), 113–140 (§ 4).CrossRefGoogle Scholar

† Comptes Rendus, 04 1914, 1012–4.Google Scholar

‡ Acta Math. 37 (1914), 193–238 (226).CrossRefGoogle Scholar

* Compare Hardy, G. H. and Ramanujan, S., “Asymptotic formulae in combinatory analysis”, Proc. London Math. Soc. (2), 17 (1918), 75–115, Lemma 4·31. (Ramanujan's Collected Papers, No. 36.)CrossRefGoogle Scholar

† Proc. Camb. Phil. Soc. 23 (1927), 675–680, Lemma 1.CrossRefGoogle Scholar

* Watson, G. N., Theory of Bessel functions (1922), 177 (8). It is at this stage that the proof follows the classical method of Wigert (loc. cit.).Google Scholar

* See, for example, Hobson, E. W., Theory of functions of a real variable, 2 (1926), 288–289.Google Scholar

† Whittaker, and Watson, , Modern analysis (1920), 246.Google Scholar

‡ Bromwich, , Theory of infinite series (1908), 453, Theorem B.Google Scholar

§ Since , it follows that (4·1) is absolutely and uniformly convergent if .Google Scholar

* Comptes Rendus, 178 (1924), 303.Google ScholarHobson, , loc. cit., 626.Google Scholar

† (P, q) denotes the greatest common factor of p and q.Google Scholar

‡ The change of order follows from Lemma 3 and the theorem quoted from Hobson, as in (3.61). If σ>7, Lemma 2 and the absolute convergence test are sufficient.7,+Lemma+2+and+the+absolute+convergence+test+are+sufficient.>Google Scholar