No CrossRef data available.
Note on propagation of classical waves: II
Published online by Cambridge University Press: 24 October 2008
Extract
1. Main results and notations. We consider Cauchy's problem for the classical wave equation in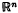 
:
with initial conditions u(0, x) = uo(x) and ∂tu(0, x) = u1 (x). In (1·1) δ and m2 stand for the Laplacian in 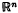and a constant respectively. Note that a second order hyper-bolic differential equation with real constants can be reduced to (1·1) ([1], p. 183). Let uj (j = 0,1) be C∞ funotions on 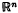whose support is contained in the closed ball BR = {xεl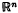; |x| ≥R} for some R > 0. In this note we shall show that the solution u(t, x) of (1·1) possesses the following properties.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 98 , Issue 2 , September 1985 , pp. 367 - 372
- Copyright
- Copyright © Cambridge Philosophical Society 1985
References
REFERENCES
[1]Courant, R. and Hilbert, D.Methods of Mathematical Physics, vol. 2 (Interscience Publishers, 1962).Google Scholar
[2]Freedlakdeb, F. G.The Wave Equation in a Curved Space-time (Cambridge University-Press, 1975).Google Scholar
[3]Gel'fand, I. M. and Shilov, G. E.Generalized Functions, vol. 1 (Academic Press, 1964).Google Scholar
[4]Kaneta, H.Note on propagation of classical waves: I. Math. Proc. Cambridge Philos. Soc. 98 (1985), 179–181.CrossRefGoogle Scholar
[5]Mizohata, S.The Theory of Partial Differential Equations (Cambridge University Press, 1973).Google Scholar
[6]Watson, G. N.A treatise on the theory of Besselfunctions (Cambridge University Press, 1922).Google Scholar