Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-05T12:42:28.454Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on natural maps of higher extension functors

Published online by Cambridge University Press:  24 October 2008

F. Oort
F. Oort
Affiliation:
Mathematisch Instituut, Nieuwe Achtergracht 121, Amsterdam (C), The Netherlands
Get access Rights & Permissions [Opens in a new window]

Extract

Hilton and Rees have proved (cf. (1), Theorem 1·3) that every natural map

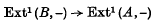
is induced by a map from A to B (or, Hom (A, B) → Next1,1 (A, B) is surjective). It follows that Ext1 (B, −) and Ext1 (A, −) are naturally isomorphic if and only if A and B are quasi-isomorphic (loc. cit., Theorem 2·6), i.e. if there exist projective objects P, Q and an isomorphism 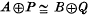. One can ask whether these theorems remain true for higher extension functors.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 59 , Issue 2 , April 1963 , pp. 283 - 286
Copyright
Copyright © Cambridge Philosophical Society 1963

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCE

(1)Hilton, P. J., and Rees, D., Natural maps of extension functors and a theorem of R. G. Swan. Proc. Cambridge Philos. Soc. 57 (1961), 489–502.CrossRefGoogle Scholar