Hostname: page-component-7bb8b95d7b-dtkg6 Total loading time: 0 Render date: 2024-09-16T12:10:05.487Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on fluctuations and the shot effect

Published online by Cambridge University Press:  24 October 2008

E. N. Rowland
E. N. Rowland
Affiliation:
Gonville and Caius College
Get access Rights & Permissions [Opens in a new window]

Extract

The present author recently published what he believed to be a proof and extension of Campbell's theorem on fluctuations. More recently a paper has been published containing a criticism of this proof. It therefore seems desirable that some parts of the proof be amplified. Further explanation of the foundations of the theory seems required, in order that it shall not appear that the theory ignores the randomness of the events, and a more detailed account of the derivation of the mean value of functions of pairs of events (i.e. sums of the type 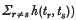) is necessary.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 34 , Issue 3 , July 1938 , pp. 329 - 334
Copyright
Copyright © Cambridge Philosophical Society 1938

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Proc. Cambridge Phil. Soc. 32 (1936), 580–97.Google Scholar

† “The shot effect for showers”, by Whittaker, J. M., Proc. Cambridge Phil. Soc. 33 (1937), 451–8CrossRefGoogle Scholar (456).

* The following argument can readily be put into formal mathematical language as was shown in the previous paper with It is regretted that a term was there inverted. The way to avoid the difficulty that the above statement about the yield of a pair of events is only an approximation and does not hold at the discontinuities is there shown by the use of and here omitted for simplicity.

* The process can be modified by introducing a division of the range of h as well as of the interval (− T 0, T 1) and it can be shown that existence of the Lebesgue integral ensures convergence of the corresponding approximations. Campbell's theorem is therefore true with Lebesgue integrals. The existence of some integral is, however, a necessary postulate for the convergence.

† “The shot effect, II”, Proc. Cambridge Phil. Soc. 33 (1937), 344–58.CrossRefGoogle Scholar

* “Fluctuation voltage in diodes and in multielectrode valves”, J. Inst. Elec. Eng. 79 (1936), No. 477, pp. 349–60.Google Scholar