No CrossRef data available.
A note on a theorem of Stanton-Weinstein on the L4-norm of spherical harmonics
Published online by Cambridge University Press: 24 October 2008
Extract
1. Let El (l = 0,1,2, …) be the eigenspaces of the Laplacian on the standard 2-sphere S2. Consider the function r2. 4: El −{0} → R given by
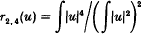
Stanton and Weinstein proved in [1] that r2, 4 was locally maximized by the ‘highest weight’ function 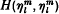 . This note is to simplify part of their proof, namely that of the negativity of
. This note is to simplify part of their proof, namely that of the negativity of 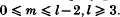 .
.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 102 , Issue 3 , November 1987 , pp. 561 - 563
- Copyright
- Copyright © Cambridge Philosophical Society 1987
References
REFERENCE
[1]Stanton, R. J. and Weinstein, A.. On the L 4 norm of spherical harmonics. Math. Proc. Cambridge Philos. Soc. 89 (1981), 343–358.CrossRefGoogle Scholar


