Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-30T19:59:41.655Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on a Divergent Series

Published online by Cambridge University Press:  24 October 2008

G. H. Hardy
G. H. Hardy
Affiliation:
Trinity CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

1. The series

is the simplest and most familiar power series whose radius of convergence is zero. It is natural to regard it as a development of the function G(z) defined, when

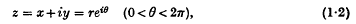
by

For

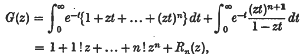
say;and

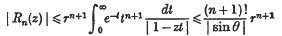
or

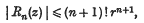
according as x is positive or negative. Thus the series (1·1) is an asymptotic series for G(z) in the sense of Poincaré.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 37 , Issue 1 , January 1941 , pp. 1 - 8
Copyright
Copyright © Cambridge Philosophical Society 1941

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* | 1 − zt|2 = 1 − 2rt cos θ + r 2t 2 has the minimum sin2θ or 1, according as cos θ is positive or negative.

* The point is to choose λn so that

is an integral function, for every positive δ, but with “little to spare”.

* That is to say, of the distant part of C′. The inequality is not satisfied near u = A.

* P(∞, η) is the region which is the limit of P(R, η) when R → ∞.

* We express a n first by an integral round a contour lying inside the circle of convergence of the series (7·1). We may deform this contour into C because f(z) is regular in P and satisfies (7·2).

† This is the definition of g k+1(z).