Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-30T19:09:03.699Z Has data issue: false hasContentIssue false
  • English
  • Français

A non-commutative Gel'fand-Naimark theorem

Published online by Cambridge University Press:  24 October 2008

Christopher J. Mulvey
Christopher J. Mulvey
Affiliation:
University of Sussex
Get access Rights & Permissions [Opens in a new window]

Extract

This paper presents a straightforward proof of the Gel'fand-Naimark theorem for non-commutative C*-algebras with identity, established by Dauns and Hofmann(2) in the context of fields of C*-algebras, by considering instead C*-algebras in categories of sheaves. The proof differs from that of (2,3,4) in obtaining an isometric *-isomorphism

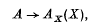
from the C*-algebra A to the C*-algebra of sections of a C*-algebra Ax in the category of sheaves on the maximal ideal space X of the centre of A, without invoking any arguments which involve completeness (3, Theorem 7·9). Instead, the results of (7) yield immediately the existence of an algebraic isomorphism, the compactness of the maximal ideal space X then being used to prove that Ax is indeed a C*-algebra in the category of sheaves on X and that the isomorphism is isometric. One recovers the representation of (2) by noting (8) that any C*-algebra in the category of sheaves on X is isomorphic to the sheaf of sections of a canonical field of C*-algebras on X.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 88 , Issue 3 , November 1980 , pp. 425 - 428
Copyright
Copyright © Cambridge Philosophical Society 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Burden, C. W. and Mulvey, C. J.Banach spaces in categories of sheaves. In Applications of Sheaves: Proceedings of the Durham Symposium, 07 1977. Lecture Notes in Mathematics 753, 169–196 (Berlin and New York: Springer, 1979).Google Scholar
(2)Dauns, J. and Hofmann, K. H.Representations of rings by sections. Mem. Amer. Math. Soc. 83 (1968).Google Scholar
(3)Hofmann, K. H.Representations of algebras by continuous sections. Bull. Amer. Math. Soc. 78 1972). 291–373.CrossRefGoogle Scholar
(4)Hofmann, K. H. and Keimel, K.Sheaf-theoretical concepts in analysis. In Applications of Sheaves: Proceedings of the Durham Symposium, 07 1977. Lecture Notes in Mathematics, 753, 415–441 (Berlin and New York: Springer, 1979).Google Scholar
(5)Johnstone, P. T.Topos Theory. L.M.S. Monographs, 10 (London and New York: Academic Press, 1977).Google Scholar
(6)Mulvey, C. J.Intuitionistic algebra and representations of rings. In Recent Advances in the Representation Theory of Rings and C*-algebras by Continuous Sections. Mem. Amer. Math. Soc. 148 (1974), 3–57.Google Scholar
(7)Mulvey, C. J.A categorical characterisation of compactness. J. London Math. Soc. (2), 17 (1978), 356–362.CrossRefGoogle Scholar
(8)Mulvey, C. J.Banach sheaves. J. Pure and Applied Algebra 17 (1980), 69–83.CrossRefGoogle Scholar
(9)Mulvey, C. J.Banach spaces over a compact space. In Categorical Topology: Berlin, 1978. Lecture Notes in Mathematics, 719, 243–249 (Berlin and New York: Springer, 1979).Google Scholar