Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-22T23:14:36.516Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-classical polynomials and the inverse theorem

Published online by Cambridge University Press:  15 December 2021

AARON BERGER ,
ASHWIN SAH ,
MEHTAAB SAWHNEY  and
JONATHAN TIDOR
AARON BERGER
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, U.S.A e-mails: [email protected], [email protected], [email protected], [email protected]
ASHWIN SAH
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, U.S.A e-mails: [email protected], [email protected], [email protected], [email protected]
MEHTAAB SAWHNEY
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, U.S.A e-mails: [email protected], [email protected], [email protected], [email protected]
JONATHAN TIDOR
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, U.S.A e-mails: [email protected], [email protected], [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we characterize when non-classical polynomials are necessary in the inverse theorem for the Gowers 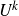$U^k$ -norm. We give a brief deduction of the fact that a bounded function on 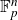$\mathbb F_p^n$ with large 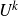$U^k$ -norm must correlate with a classical polynomial when 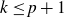$k\le p+1$ . To the best of our knowledge, this result is new for 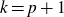$k=p+1$ (when 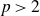$p>2$ ). We then prove that non-classical polynomials are necessary in the inverse theorem for the Gowers 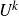$U^k$ -norm over 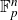$\mathbb F_p^n$ for all 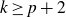$k\ge p+2$ , completely characterising when classical polynomials suffice.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 173 , Issue 3 , November 2022 , pp. 525 - 537
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Berger, Sah, Sawhney, and Tidor were supported by NSF Graduate Research Fellowship Program DGE-1745302.

References

N., Alon and R., Beigel. Lower bounds for approximations by low degree polynomials over $\mathbb{Z}/m\mathbb{Z}$ . Proceedings 16th Annual IEEE Conference on Computational Complexity pp. 184–187.Google Scholar
V., Bergelson, T., Tao, and T., Ziegler. An inverse theorem for the uniformity seminorms associated with the action of $\mathbb F^\infty_p$ . Geom. Funct. Anal. 19 (2010), 1539–1596.Google Scholar
B., Green and T., Tao. The distribution of polynomials over finite fields, with applications to the Gowers norms.. Contrib Discrete Math. 4 (2009), 1–36.Google Scholar
S., Lovett, R., Meshulam and A., Samorodnitsky. Inverse conjecture for the Gowers norm is false. Theory Comput. 7 (2011), 131–145.Google Scholar
A., Samorodnitsky. Low-degree tests at large distances. STOC’07 Proceedings of the 39th Annual ACM Symposium on Theory of Computing ACM, New York, 2007, pp. 506–515.CrossRefGoogle Scholar
T., Tao and T., Ziegler. The inverse conjecture for the Gowers norm over finite fields via the correspondence principle. Analysis & PDE 3 (2010), 1–20.Google Scholar
T., Tao and T., Ziegler. The inverse conjecture for the Gowers norm over finite fields in low characteristic. Ann. Comb. 16 (2012), 121–188.Google Scholar