No CrossRef data available.
Published online by Cambridge University Press: 23 May 2023
Let 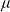 $\mu$ be a Radon measure on the nth Heisenberg group
$\mu$ be a Radon measure on the nth Heisenberg group 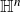 ${\mathbb{H}}^n$. In this note we prove that if the
${\mathbb{H}}^n$. In this note we prove that if the 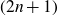 $(2n+1)$-dimensional (Heisenberg) Riesz transform on
$(2n+1)$-dimensional (Heisenberg) Riesz transform on 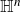 ${\mathbb{H}}^n$ is
${\mathbb{H}}^n$ is 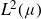 $L^2(\mu)$-bounded, and if
$L^2(\mu)$-bounded, and if 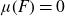 $\mu(F)=0$ for all Borel sets with
$\mu(F)=0$ for all Borel sets with 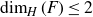 ${\text{dim}}_H(F)\leq 2$, then
${\text{dim}}_H(F)\leq 2$, then 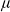 $\mu$ must have
$\mu$ must have 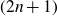 $(2n+1)$-polynomial growth. This is the Heisenberg counterpart of a result of Guy David from [Dav91].
$(2n+1)$-polynomial growth. This is the Heisenberg counterpart of a result of Guy David from [Dav91].
Supported by Spanish Ministry of Economy and Competitiveness, through the María de Maeztu Programme for Units of Excellence in R&D (grant MDM-2014-0445). Partially supported by the Catalan Agency for Management of University and Research Grants (grant 2017-SGR-0395), and by the Spanish Ministry of Science, Innovation and Universities (grant MTM-2016-77635-P).
Supported by The Maxwell Institute Graduate School in Analysis and its Applications, a Centre for Doctoral Training funded by the UK Engineering and Physical Sciences Research Council (grant EP/L016508/01), the Scottish Funding Council, Heriot-Watt University and the University of Edinburgh.
Partially supported by the grant 346300 for IMPAN from the Simons Foundation and the matching 2015-2019 Polish MNiSW fund.