Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-07T21:03:58.391Z Has data issue: false hasContentIssue false
  • English
  • Français

The multiplicative process in semiconductor radiation detectors. A practical application of Good's theorem in the theory of branching processes

Published online by Cambridge University Press:  24 October 2008

Iwao Ogawa  and
Masao Furukawa
Iwao Ogawa
Affiliation:
Department of Physics, Rikkyo University, Toshima-Ku, Tokyo, Japan
Masao Furukawa
Affiliation:
Department of Physics, Rikkyo University, Toshima-Ku, Tokyo, Japan
Get access Rights & Permissions [Opens in a new window]

Abstract

The electron avalanche that takes place within an internally amplifying semiconductor radiation detector has been analysed statistically, treating the process as an example of multi-dimensional branching processes. By extending the result obtained from Good's theorem to the case of continuous variable, an integral equation is derived for the generating function of the probability that a single primary electron-hole pair, formed at a depth x, induces an avalanche consisting of n pairs. On the basis of this equation, expressions are deduced for the mean value 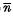and the standard deviation σ of the total number n of pairs in an avalanche induced by n0 primary pairs produced at x, as well as the probability w(x, n0, n) of getting an avalanche of ‘size’ n. In particular cases these expressions lead to various simple relations of practical importance.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 64 , Issue 1 , January 1968 , pp. 203 - 214
Copyright
Copyright © Cambridge Philosophical Society 1968

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Huth, G. C, Bergeson, H. E. and Trice, J. B.Rev. Sci. Iustrum. 34 (1963), 1283.Google Scholar
(2)Huth, G. C, Trice, J. B. and Mckinney, R. A.Rev. Sci. lustrum. 35 (1964), 1220.CrossRefGoogle Scholar
(3)Huth, G. C, Trice, J. B. and Shannon, J. A.IEEE Trans. Nucl. Sci. NS-12, no. 1 (1965), 275.Google Scholar
(4)Huth, G. C.IEEE Trans. Nucl. Sci. NS-13, no. 1 (1966), 36.CrossRefGoogle Scholar
(5)Harris, T. E.The theory of branching processes, Die Grundlagen der mathematischen Wissenschaften, Bd. 119 (Springer Verlag; Berlin, 1963).CrossRefGoogle Scholar
(6)McKay, K. G. and Mcafee, K. B.Phys. Rev. 91 (1953), 1079.CrossRefGoogle Scholar
(7)McKay, K. G.Phys. Rev. 94 (1954), 877.CrossRefGoogle Scholar
(8)Miller, S. L.Phys. Rev. 99 (1955), 1234.CrossRefGoogle Scholar
(9)Ogawa, I.Nucl. lustrum. & Methods 49 (1967), 325.CrossRefGoogle Scholar
(10)Townsend, J. S.Phil. Mag. 3 (1902), 557; 6 (1903), 389, 598.CrossRefGoogle Scholar
(11)Loeb, L. B.Fundamental processes of electrical discharge in gases, chapter ix (John Wiley and Sons, Inc.; New York, 1939).Google Scholar
(12)Feller, W.An introduction to probability theory and its application, second edition (John Wiley and Sons, Inc.; New York, 1957).Google Scholar
(13)Good, I. J.Proc. Cambridge Philos. Soc. 51 (1955), 240.Google Scholar
(14)Good, I. J.Proc. Cambridge Philos. Soc. 56 (1960), 367.CrossRefGoogle Scholar
(15)Watanabe, Y.Semiconductors and transistors (in Japanese), vol. n, chapter 10 (Ohm-Sha; Tokyo, 1963).Google Scholar
(16)Chynoweth, A. G.Phys. Rev. 109 (1958), 1537.Google Scholar
(17)Tager, A. S.Fizika Tverdovo Tela 6 (1964), 2418; translation, Soviet Physics solid St. 6 (1965), 1919.Google Scholar
(18)Otter, R.Ann. Math. Statist. 20 (1949), 206.Google Scholar
(19)Furry, W. H.Phys. Rev. 52 (1937), 569.Google Scholar