Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T11:21:55.563Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiplicative norms on Banach algebras

Published online by Cambridge University Press:  24 October 2008

R. E. Edwards
R. E. Edwards
Affiliation:
Birkbeck CollegeLondon
Get access Rights & Permissions [Opens in a new window]

Extract

1. Mazur(1) has shown that any normed algebra A over the real field in which the norm is multiplicative in the sense that

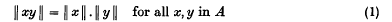
is equivalent (i.e. algebraically isomorphic and isometric under one and the same mapping) to one of the following algebras: (i) the real numbers, (ii) the complex numbers, (iii) the real quaternions, each of these sets being regarded as normed algebras over the real field. Completeness of A is not assumed by Mazur. A relevant discussion is given also in Lorch (2).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 47 , Issue 3 , July 1951 , pp. 473 - 474
Copyright
Copyright © Cambridge Philosophical Society 1951

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Mazur, S.Sur les anneaux linéaires. C.R. Acad. Sci., Paris, 207 (1938), 1025–7.Google Scholar
(2)Lorch, E. R.The theory of analytic functions in normed abelian vector rings. Trans. American Math. Soc. 54 (1943), 414–25.CrossRefGoogle Scholar
(3)Hille, E.Functional analysis and semigroups. American Mathematical Society Colloquium Publications, vol. 31 (New York, 1948).Google Scholar