Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-30T22:07:49.735Z Has data issue: false hasContentIssue false
  • English
  • Français

The motivic cohomology of BSOn

Published online by Cambridge University Press:  11 April 2017

MASANA HARADA  and
MASAYUKI NAKADA
MASANA HARADA
Affiliation:
Department of Mathematics, Kyoto University, Kyoto606-8502, Japan. e-mail: [email protected]
MASAYUKI NAKADA
Affiliation:
Kobe University Secondary School, 5-11-1Sumiyoshiyamate, Higashinada-ku, Kobe, Hyogo658-0063Japan. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We will determine the motivic cohomology H*,* (BSOn, 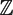$\mathbb{Z}$/2) with coefficients in 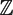$\mathbb{Z}$/2 of the classifying space of special orthogonal groups SOn over the complex numbers 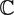$\mathbb{C}$.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 164 , Issue 3 , May 2018 , pp. 461 - 471
Copyright
Copyright © Cambridge Philosophical Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Edidin, D. and Graham, W. Characteristic classes and quadratic bundles. Duke Math. J. 78 (1995), 277–299.Google Scholar
[2] Edidin, D. and Graham, W. Equivariant intersection theory. Invent. Math. 131 (1998), 595–634.CrossRefGoogle Scholar
[3] Field, R. The Chow ring of the classifying space BSO(2n,$\mathbb{C}$). J. of Algebra 350 (2012), 330–339.CrossRefGoogle Scholar
[4] Field, R. The Chow ring of the symmetric space Gl(2n,$\mathbb{C}$)/SO(2n,$\mathbb{C}$). J. of Algebra 349 (2012), 364–371.Google Scholar
[5] Grothendieck, A. Torsion homologique et sections rationelles. Séminaire Claude Chevalley. tome 3, exp. 5 (1958).Google Scholar
[6] Inoue, K. and Yagita, N. The complex cobordism of BSO n. Kyoto J. Math. 50 (2010), 307–324.Google Scholar
[7] Kono, A. and Yagita, N. Brown–Peterson and ordinary cohomology theories of classifying spaces for compact Lie groups. Trans. Amer. Math. Soc. 339 (1993), 781–798.CrossRefGoogle Scholar
[8] Molina, L. and Vistoli, A. On the Chow rings of classifying spaces for classical groups. Rend. Sem. Mat. Univ. Padova 116 (2006), 271–298.Google Scholar
[9] Morel, F. and Voevodsky, V. $\mathbb{A}$1-homotopy theory of schemes. Publ. Math. IHES 90 (1999), 45–143.CrossRefGoogle Scholar
[10] Orlov, D., Vishik, A. and Voevodsky, V. An exact sequence for K M*/2 with applications to quadratic forms. Ann. of Math. 165 (2007), 1–13.Google Scholar
[11] Pandraharipande, R. Equivarinat Chow rings for O(k), SO(2k+1) and SO(4). J. Reine Angew. Math. 496 (1998), 131–148.Google Scholar
[12] Panin, I. Oriented cohomology theories of algebraic varieties. II (After I. Panin and A. Smirnov). Homology, Homotopy Appl. 11 (2009), 349–405.Google Scholar
[13] Soulynin, A. A. Gysin homomorphism in generalised cohomology theories. St. Petersburg Math. J. 17 (2006), 511–525.Google Scholar
[14] Suslin, A. and Voevodsky, V. Bloch-Kato conjecture and motivic cohomology with finite coefficients, volume 548 of NATO Sci. Ser. C Math. Phys. Sci. (Kluwer Acad. Publ, Dordrecht, 2000) 117–189.Google Scholar
[15] Totaro, B. Torsion algebraic cycles and complex cobordism. J. Amer. Math. Soc. 10 (1997), 467–493.Google Scholar
[16] Totaro, B. The Chow ring of a classifying space. Algebraic K-theory (Seattle, WA, 1997), Amer. Math. Soc, 67 (1999), 249–281.Google Scholar
[17] Vezzosi, G. On the Chow ring of the classifying stack of ${PGL}_{3,\mathbb{C}}$. J. Reine Angew. Math. 523 (2000), 1–54.Google Scholar
[18] Voevodsky, V. The Milnor conjecture. Preprint (1996).Google Scholar
[19] Voevodsky, V. Motivic cohomolgy with $\mathbb{Z}$/2-coefficients. Publ. Math. IHES 98 (2003), 59–104.CrossRefGoogle Scholar
[20] Voevodsky, V. Reduced power operations in motivic cohomology. Publ. Math. IHES 98 (2003), 1–57.Google Scholar
[21] Stephen, W. Wilson. The complex cobordism of BO(n). J. London Math. Soc. 29 (1984), 352–366.Google Scholar
[22] Yagita, N. Examples for the mod p motivic cohomology of classifying spaces. Trans. AMS. 355 (2003), 4427–4450.Google Scholar
[23] Yagita, N. Applications of Atiyah-Hirzebruch spectral sequence for motivic cobordism. Proc. London Math. Soc. 90 (2005), 783–816.CrossRefGoogle Scholar
[24] Yagita, N. Coniveau filtration of cohomology of groups. Proc. London Math. Soc. 101 (2010), 179–206.Google Scholar