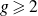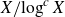Fix an integer $g \geqslant 2$ . Every positive integer $a \in \mathbb N$ has a base g representation, i.e. it can be uniquely written as

(1) \begin{equation}a = \overline{a_n a_{n-1} \ldots a_0} = \sum_{i=0}^n g^i a_i, \, \text{ where }a_i \in \{0, 1, \ldots, g-1\} \text{ and }a_n\neq 0.\end{equation}

A number $a \in \mathbb N$ with representation (1) is called a base g palindrome if $a_i = a_{n-i}$ holds for all $i=0, \ldots, n$ . Baxter, Cilleruelo and Luca [ Reference Cilleruelo, Luca and Baxter3 ] studied additive properties of the set of base g palindromes. Improving on a result of Banks [ Reference Banks2 ], they showed that every positive integer can be written as a sum of three palindromes, provided that $g\geqslant 5$ . The cases $g=2, 3, 4$ were later covered by Rajasekaran, Shallit and Smith [ Reference Rajasekaran, Shallit and Smith4 , Reference Rajasekaran, Shallit and Smith5 ]. Baxter, Cilleruelo and Luca also showed that the number of integers at most X which are sums of two palindromes is at least $X e^{-c_1\sqrt{\log X}}$ and at most $c_2 X$ , for some constants $c_1 \gt 0$ and $c_2 \lt 1$ depending on g, and asked whether a positive fraction of integers can be written as a sum of two base g palindromes. This was later reiterated by Green in his list of open problems as Problem 95. We answer this question negatively:

Theorem 1. For any integer $g \geqslant 2$ there exists a constant $c \gt 0$ such that

\begin{align*} \# \{ n \lt X:\, n \text{ is a sum of two base }g\text{ palindromes} \} \leqslant \frac{X}{\log^{c} X}, \end{align*}

for all large enough X.

It is an interesting open problem to close the gap between this result and the lower bound of Baxter, Cilleruelo and Luca [ Reference Cilleruelo, Luca and Baxter3 ]. We now proceed to the proof.

For $n \geqslant 1$ , let $P_n$ be the set of base g palindromes with exactly n digits and $P = \bigcup_{n\geqslant 1}P_n$ be the set of all base g palindromes. Note that

\begin{align*}|P_n| = \begin{cases} g^{n/2}-g^{n/2-1}, \, n\text{ is even,}\\ g^{(n+1)/2}-g^{(n-1)/2}, \,n\text{ is odd.}\end{cases}\end{align*}

For an integer $N \geqslant 1$ , we write $[N] = \{0, 1, \ldots, N-1\}$ . For $A, B \subset \mathbb Z$ we let $A+B = \{a+b, \,a\in A, \,b \in B\}$ denote the sumset of A and B. Let $k \geqslant 1$ be sufficiently large and let $X = g^k$ , it is enough to consider numbers X of this form only. With this notation, our goal is to upper bound the size of the intersection $(P + P) \cap [X]$ . We have

\begin{align*}(P + P) \cap [X] = \bigcup_{k \geqslant n \geqslant m \geqslant 1} (P_n + P_m) \cap [X]\end{align*}

and so we can estimate

(2) \begin{equation}|(P+P) \cap [X]| \leqslant \sum_{k \geqslant n \geqslant m \geqslant 1} |P_n + P_m|.\end{equation}

We have $|P_n| \leqslant g^{(n+1)/2}$ , $|P_{m}| \leqslant g^{ (m+1)/2}$ so using the trivial bound $|P_n+P_m| \leqslant |P_n| |P_m|$ we can immediately get rid of the terms where m is small:

(3) \begin{align}\sum_{\substack{k \geqslant n \geqslant m \geqslant 1\\ m \leqslant k-\gamma \log k}} |P_n + P_m| & \leqslant \sum_{k \geqslant n \geqslant 1} |P_n| \cdot \sum_{m \leqslant k-\gamma \log k} |P_m|\\ & \leqslant \sum_{k \geqslant n \geqslant 1} |P_n| \cdot 4 g^{(k+1)/2 -\gamma \log k/2}\nonumber\\& \leqslant 16 g^{k+1 - \gamma \log k /2} \lesssim \frac{X}{k^{\gamma \log g/2}} \sim \frac{X}{(\log X)^{\gamma \log g/2}},\nonumber\end{align}

where $\gamma \gt 0$ is a small constant which we will choose. Now we focus on a particular sumset $P_n + P_m$ from the remaining range. Write $m = n-d$ for some $d \geqslant 0$ .

For an integer $a = \overline{a_n \ldots a_0} $ let $r(a) = \overline{a_0 \ldots a_n}$ be the integer with the reversed digit order in base g (we allow some leading zeros here). For $d\geqslant 0$ define

\begin{align*}a = \overline{1 \underbrace{0\ldots 0}_{d}1 }, \, b = \overline{0 \underbrace{0\ldots 0}_{d}0}, \,a' = \overline{0 \underbrace{\ell \ldots \ell}_{d} 0}, \, b' = \overline{\underbrace{0 \ldots 0}_{d} 11},\end{align*}

where we denoted $\ell = g-1$ . These strings are designed to satisfy the following:

(4) \begin{equation}a + b = a' + b' \,\text{ and }\, g^{d} r(a) + r(b) = g^{d} r(a') + r(b').\end{equation}

Indeed, note that

\begin{align*}a' = \sum_{i=1}^d g^{i}\ell = g^{d+1}-g = (g^{d+1}+1) + 0 - (g+1) = a+b-b'\end{align*}

and

\begin{align*}g^d r(a') = g^d a' = g^{2d+1}-g^{d+1} = g^{d}(g^{d+1}+1) + 0 - (g^{d+1}+g^d) = g^d r(a) + r(b) - r(b').\end{align*}

We claim that the fact that (4) holds for some a, b, a ^′, b ^′ forces the sumset $P_n + P_{n-d}$ to be small. Roughly speaking, whenever palindromes $p \in P_n$ and $q \in P_{n-d}$ contain strings a and b on the corresponding positions, we can swap a with a ^′ and b with b ^′ to obtain a new pair of palindromes $p' \in P_n$ and $q' \in P_{n-d}$ with the same sum $p'+q'=p+q$ . A typical pair (p, q) will have $\gtrsim C^{-d} n$ disjoint substrings (a, b) and so we can do the swapping in $\gtrsim \exp(C^{-d} n)$ different ways. So a typical sum $p+q \in P_n + P_{n-d}$ has lots of representations and this means that the sumset has to be small.

Denote $t = [{n}/{3(d+2)}]$ . For $p = \overline{p_0 p_1 \ldots p_1 p_0} \in P_n$ and $q = \overline{q_0 q_1 \ldots q_1 q_0} \in P_{n-d}$ let S(p, q) denote the number of indices $1 \leqslant j \leqslant t$ such that

(5) \begin{equation}\overline{p_{(d+2) j + d+1} p_{(d+2)j+d} \ldots p_{(d+2)j+1} p_{(d+2)j}} = a,\end{equation}

(6) \begin{equation}\overline{q_{(d+2) j + d+1} q_{(d+2)j+d} \ldots q_{(d+2)j+1} q_{(d+2)j}} = b,\end{equation}

i.e. the segments of digits of p and q in the interval $[(d+2)j, (d+2)j +d+1]$ are precisely a and b.

Proof. Draw (p, q) uniformly at random from $P_n \times P_{n-d}$ . Then S(p, q) is a sum of t i.i.d Bernoulli random variables with mean $g^{-2(d+2)}$ . So the expectation $\mathbb E_{p,q} S(p, q)$ is given by $\mu = t g^{-2(d+2)}$ and by Chernoff bound (see e.g. [ Reference Alon and Spencer1 , appendix A]),

\begin{align*} \Pr[S(p, q) \leqslant \mu/2] \leqslant \exp\left(- \mu / 8\right) = \exp\left( - \frac{t}{8 g^{2d+4} } \right). \end{align*}

Now we observe that for any $p=\overline{p_0 p_1 \ldots p_1 p_0} \in P_n$ , $q = \overline{q_0 q_1 \ldots q_1 q_0} \in P_{n-d}$ , the sum $s=p+q$ has at least $2^{S(p,q)}$ distinct representations $s = p'+q'$ for $(p', q') \in P_n \times P_{n-d}$ . Indeed, let $j_1 \lt \ldots \lt j_u$ be an arbitrary collection of indices such that (5) and (6) hold for $j=j_1, \ldots, j_u$ . Let p ^′ and q ^′ be obtained from p and q by replacing the a and b-segments on positions $j_1, \ldots, j_u$ by a ^′ and b ^′ and replacing r(a) and r(b)-segments on the symmetric positions by r(a ^′) and r(b ^′), respectively. Then we claim that $p' \in P_n$ , $q' \in P_{n-d}$ and $p'+q'=p+q$ . Indeed, more formally, we can write

\begin{align*}p' = p + \sum_{i=1}^u g^{(d+2) j_i} (a' - a) + g^{n-(d+2) j_i - d-1} (r(a') - r(a)),\end{align*}

\begin{align*}q' = q + \sum_{i=1}^u g^{(d+2) j_i} (b' - b) + g^{(n-d)-(d+2) j_i - d-1} (r(b') - r(b)),\end{align*}

and so (4) implies that $p+q=p'+q'$ . Since we can choose $j_1 \lt \cdots \lt j_u$ to be an arbitrary subset of S(p,q) indices, we get $2^{S(p, q)}$ different representations $p+q=p'+q'$ .

Using this and Proposition 1 we get

\begin{align*} |P_n + P_{n-d}| & \leqslant \# \left\{p+q \,|\, S(p, q) \geqslant \frac{t}{2g^{2d+4}}\right\} + \# \left\{p+q \,|\, S(p, q) \leqslant \frac{t}{2g^{2d+4}}\right\}\\& \leqslant 2^{- \frac{t}{2g^{2d+4}}} |P_n| |P_{n-d}| + \exp\left(- \frac{t}{8g^{2d+4}}\right) |P_n| |P_{n-d}|\\& \leqslant 2 \exp\left(- \frac{n}{30(d+2) g^{2d+4}}\right) |P_n| |P_{n-d}|.\end{align*}

Using this bound we can estimate the part of (2) which was not covered by (3):

\begin{align*}\sum_{k \geqslant n \geqslant m \geqslant k-\gamma \log k} |P_n + P_m| & \leqslant \sum_{k \geqslant n \geqslant k-\gamma \log k} \sum_{d = 0}^{\gamma \log k} |P_n + P_{n-d}|\\& \leqslant \sum_{k \geqslant n \geqslant k-\gamma \log k} \sum_{d = 0}^{\gamma \log k} 2 \exp\left(- \frac{n}{30(d+2) g^{2d+4}}\right) |P_n| |P_{n-d}|\\&\leqslant \sum_{k\geqslant n \geqslant k-\gamma \log k} 2 \exp\left( - \frac{n}{k^{3 \gamma \log g}} \right) g^{k+1}\end{align*}

so if we take, say, $\gamma = {1}/{4 \log g}$ then this expression is less than, say, $k^{-1} g^k \lesssim {X}/{\log X}$ provided that k is large enough. Combining this with (3) gives $|(P+P) \cap [X]| \leqslant {X}/{(\log X)^{0.1}}$ for large enough X (the proof actually gives $1/4-\varepsilon$ instead of $0.1$ here).