Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T13:12:31.016Z Has data issue: false hasContentIssue false
  • English
  • Français

Moduli spaces of algebraic curves with rational maps

Published online by Cambridge University Press:  24 October 2008

Herbert Lange
Herbert Lange
Affiliation:
Math. Institut, Göttingen
Get access Rights & Permissions [Opens in a new window]

Extract

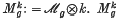Let ℳg be the coarse moduli scheme of curves of genus g. For an algebraically closed field k define is a quasiprojective algebraic variety over k, its dimension being 3g – 3 for g ≥ 2, 1 for g = 1, and 0 for g = 0. It can be considered as the moduli variety for the classes of birationally equivalent curves of genus g over k. For 0 < g, g′ and n ≥ 1 let 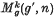be the subset of those points of whose corresponding curves possess a rational map of degree n into a curve of genus g′ over k.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 78 , Issue 2 , September 1975 , pp. 283 - 292
Copyright
Copyright © Cambridge Philosophical Society 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Baily, W. L.On the moduli of Jacobian varieties and curves, Contr. to function theory, Tata Institut. Bombay (1960).Google Scholar
(2)Grothendieck, A.Éléments de géometrie algébrique, Inst. Hautes Études sci. Publ. Math.Google Scholar
(3)Kuranishi, M.Deformations of compact complex manifolds, Les presses de l'université de Montréal, (1971).Google Scholar
(4)Lange, H. Die Mannigfaltigkeiten der Körper vom Geschlecht 2 mit elliptischem Teilkörper (Göttingen 1970 (Thesis)).Google Scholar
(5)Lange, H.Über die Modulschema der Kurven vom Geschlecht 2 mit 1, 2 oder 3 Weierstraβpunkten, to appear in J. Reine Angew Math.Google Scholar
(6)Lange, H.Über die Modulvarietät der Kurven vom Geschlecht 2, to appear in J. Reine Angew Math.Google Scholar
(7)Lapin, A. I.On subfields of hyperelliptic fields I, Izv. Akad. Nauk SSSR Ser. Mat. 28 (1964).Google Scholar
(8)Manin, J. I.Ramified coverings of algebraic curves, Izv. Akad. Nauk SSSR Ser. Mat. 25 (1961).Google Scholar
(9)Mumford, D.Geometric invariant theory (Springer Verlag, 1965).Google Scholar
(10)Tamme, G.Teilkörper höheren Geschlechts eines algebraischen Funktionenkörpers, Arch. Math. (Basel) 23 (1972).CrossRefGoogle Scholar