A well-known result of classical function theory, Jensen's formula, expresses the integral around a circle of the log modulus of a meromorphic function in terms of the log modulus of the zeros and poles of that function lying inside the circle. Explicitly, if F is a meromorphic function on the unit disc {ω ε ℂ: |ω| < 1} and F(0) = 1, then, for 0 < r < 1,

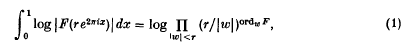
where ordωF is the order of F at ω. The purpose of this note is to observe that a formula analogous to (1) holds when F is replaced by a modular function for SL2(ℤ) and the integral by a suitable double integral over a fundamental domain. We shall derive this modular variant of Jensen's formula from the usual version by applying the Rankin-Selberg method and the first Kronecker limit formula. The argument admits some extension to Fuchsian groups other than SL2(ℤ), and to modular forms of weight other than zero; this point will be discussed later.