The Minkowski–Hlawka theorem† asserts that, if S is any n-dimensional star body, with the origin o as centre, and with volume less than 2ζ(n), then there is a lattice of determinant 1 which has no point other than o in S. One of the methods used to prove this theorem splits up into three stages, (a) A function ρ(x) is considered, and it is shown that some suitably defined mean value of the sum

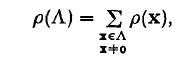
taken over a suitable set of lattices Λ of determinant 1, is equal, or approximately equal, to the integral

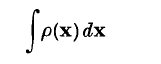
over the whole space. (b) By taking ρ(x) to be equal, or approximately equal, to

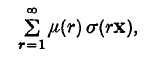
where σ(x) is the characteristic function of S, and μ(r) is the Möbius function, it is shown that a corresponding mean value of the sum

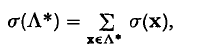
where Λ* is the set of primitive points of the lattice Λ, is equal, or approximately equal, to