Published online by Cambridge University Press: 04 December 2014
We prove that the coefficients of the mock theta functions
and
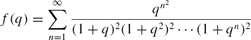 \begin{eqnarray*}
f(q) = \sum_{n=1}^{\infty} \frac{ q^{n^2}}{(1+q)^2 (1+q^2)^2 \cdots (1+q^n)^2 }
\end{eqnarray*}
possess no linear congruences modulo 3. We prove similar results for the moduli 2 and 3 for a wide class of weakly holomorphic modular forms and discuss applications. This extends work of Radu on the behavior of the ordinary partition function.
\begin{eqnarray*}
f(q) = \sum_{n=1}^{\infty} \frac{ q^{n^2}}{(1+q)^2 (1+q^2)^2 \cdots (1+q^n)^2 }
\end{eqnarray*}
possess no linear congruences modulo 3. We prove similar results for the moduli 2 and 3 for a wide class of weakly holomorphic modular forms and discuss applications. This extends work of Radu on the behavior of the ordinary partition function.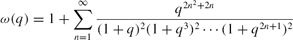 \begin{eqnarray*}
\omega(q)=1+\sum_{n=1}^\infty \frac{q^{2n^2+2n}}{(1+q)^2(1+q^3)^2\cdots (1+q^{2n+1})^2}
\end{eqnarray*}
\begin{eqnarray*}
\omega(q)=1+\sum_{n=1}^\infty \frac{q^{2n^2+2n}}{(1+q)^2(1+q^3)^2\cdots (1+q^{2n+1})^2}
\end{eqnarray*}