The minimum of a non-homogeneous binary cubic form
Published online by Cambridge University Press: 24 October 2008
Extract
1. Let f(x, y) = ax3 + bx2y + cxy2 + dy3 be a binary cubic form with real coefficients. According as the discriminant D = b2c2+ 18abcd − 4ac3 − 4db3 − 27a2d2 satisfies D ≥ 0 or D < 0, the form f(x, y) can be factorized into either three real, or one real and two conjugate complex, linear factors. A form f1(x, y) is said to be equivalent to f2(x, y) if there is an integral unimodular substitution on the variables x, y transforming f1(x, y) into f2(x, y). Thus f2(x, y) is equivalent to f1(x, y) and, in fact, the set of all forms with given discriminant can be divided into classes of equivalent forms. Davenport (3) has specified a member of each class which satisfies
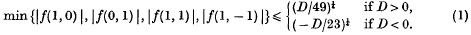
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 48 , Issue 3 , July 1952 , pp. 392 - 401
- Copyright
- Copyright © Cambridge Philosophical Society 1952
References
REFERENCES
- 3
- Cited by


