No CrossRef data available.
Published online by Cambridge University Press: 30 August 2016
In this paper we develop a notion of measure theory over boolean toposes reminiscent of the theory of von Neumann algebras. This is part of a larger project to study relations between topos theory and noncommutative geometry. The main result is a topos theoretic version of the modular time evolution of von Neumann algebras which take the form of a canonical 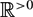 $\mathbb{R}^{>0}$-principal bundle over any integrable locally separated boolean topos.
$\mathbb{R}^{>0}$-principal bundle over any integrable locally separated boolean topos.