Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-27T01:51:18.856Z Has data issue: false hasContentIssue false
  • English
  • Français

The Markov branching process with density-independent catastrophes I. Behaviour of extinction probabilities

Published online by Cambridge University Press:  24 October 2008

Anthony G. Pakes
Anthony G. Pakes
Affiliation:
Department of Mathematics, University of Western Australia, Nedlands, W.A. 6009, Australia
Get access Rights & Permissions [Opens in a new window]

Extract

Let (Xt: t ≥ 0) be the Markov branching process (MBP) with a density independent catastrophe component. It is denned to be the Feller process on the non-negative integers having the generator

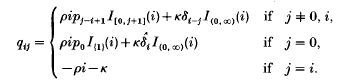
Here {pj} is the offspring distribution which satisfies p1 = 0 and p0 < 1, ρ is the per capita birth rate, κ is the rate of occurrence of catastrophe events, {δj: j ≥ 0} is the decrement distribution and 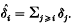. Thus Xt can be interpreted as the size of a population in which individuals reproduce according to the rules of a MBP – see Athreya and Ney[1], chap, III – and where there is an external and independent Poisson process of catastrophe events, κ per unit time, and if j < i each such event reduces the population size by j with probability δj. Usually we assume that δ0 = 0 on the basis that a catastrophe always reduces the population size. Let f(s) = Σpjsj and assume that 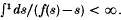. This ensures that the MBP obtained by setting κ = 0 is regular ([1], p. 105) and hence (Xt) is the unique Markov process corresponding to the above generator when κ > 0.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 103 , Issue 2 , March 1988 , pp. 351 - 366
Copyright
Copyright © Cambridge Philosophical Society 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Athreya, K. B. and Ney, P. E.. Branching Processes (Springer-Verlag, 1972).Google Scholar
[2]Embrechts, P., Goldie, C. M. and Veraverbeke, N.. Subexponentiality and infinite divisibility. Z. Wahrsch. 49 (1979), 335–347.CrossRefGoogle Scholar
[3]Feller, W.. An introduction to Probability Theory and its Applications, vol. I, 3rd ed. (Wiley, 1968).Google Scholar
[4]Goldie, C. M.. Subexponential distributions and dominated-variation tails. J. Appl. Prob. 15 (1978), 440–442.CrossRefGoogle Scholar
[5]Khan, L. V.. Limit theorems for Galton–Watson branching processes with migration. Siberian Math. J. 21 (1980), 283–292.CrossRefGoogle Scholar
[6]Pakes, A. G.. Markov branching processes with immigration. Sankhyā 37A (1975), 129–138.Google Scholar
[7]Pakes, A. G.. The Markov branching process with density independent catastrophes, II. The population size. In preparation (1987).Google Scholar
[8]Pakes, A. G.. Asymptotic results for the extinction time of Markov branching processes allowing emigration. I. Random walk decrements. Submitted to Adv. Appl. Prob. (1987).Google Scholar
[9]Stoyan, D.. Comparison Methods for Queues and other Stochastic Models (Wiley, 1983).Google Scholar
[10]Tweedie, R. L.. Criteria for rates of convergence of Markov chains, with application to queueing and storage theory. In Probability, Statistics and Analysis, London Math. Soc. Lecture Note Series, vol. 79 (Cambridge University Press 1983), pp. 260–276.Google Scholar