Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T14:07:48.420Z Has data issue: false hasContentIssue false
  • English
  • Français

A many-variable Landau-Kolmogorov inequality

Published online by Cambridge University Press:  24 October 2008

Khristo N. Boyadzhiev
Khristo N. Boyadzhiev
Affiliation:
Institute of Mathematics, Bulgarian Academy of Sciences
Get access Rights & Permissions [Opens in a new window]

Extract

The Landau–Kolmogorov inequality

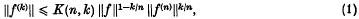
where ‖.‖ is the ‘sup’ norm, is well known and has many interesting applications and generalizations (see [1, 4–7, 13, 16]). Its study was initiated by Landau[10] and Hadamard [8] (the case n = 2). Kolmogorov [9] succeeded in finding in explicit form the best possible constants K(n, k) = Cn, k in (1) for functions on the whole real line R. The best constants 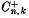for the half line R+ are not known in explicit form except for n = 2, 3, 4, but an algorithm exists for their computation (Schoenberg and Cavaretta [15]).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 101 , Issue 1 , January 1987 , pp. 123 - 129
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bollobás., B.The spatial numerical range and powers of an operator. J. London Math. Soc. (2), 7 (1973), 435–440.Google Scholar
[2]Boyadzhiev., K. N.Commuting one-parameter groups of operators, operator and functional inequalities and the Fuglede–Putnam theorem. C. R. Acad. Bulgare Sci. 38 (1985), no. 1, 19–22.Google Scholar
[3]Boyadzhiev., K. N.Commuting C 0 groups and the Fuglede–Putnam theorem. Studia Math 81 (1985), 303–306.Google Scholar
[4]Certain, M. W. and Kurtz., T. G.Landau–Kolmogorov inequalities for semigroups. Proc. Amer. Math. Soc. 63 (1977), 226–230.Google Scholar
[5]Chernoff., P. R.Optimal Landau–Kolmogorov inequalities for dissipative operators in Hilbert and Banach spaces. Adv. in Math. 34 (1979), 137–144.CrossRefGoogle Scholar
[6]Ditzian., Z.Some remarks on inequalities of Landau and Kolmogorov. Aequationes Math. 12 (1975), 145–151.CrossRefGoogle Scholar
[7]Gorny., A.Contribution à l'étude des fonctions dérivables d'une variable réele. Acta Math. 71 (1939), 317–358.Google Scholar
[8]Hadamard., J.Sur le module maximum d'une fonction et des ses dérivées. C. R. Soc. Math. France 41 (1914), 68–72.Google Scholar
[9]Kolmogorov., A. N.On inequalities between the upper bounds of the successive derivatives of an arbitrary function on an infinite interval. Uchen. Zap. Moskov. Gos. Univ. Mat. 30 (1939), no. 3, 3–13; Amer. Math. Soc. Translations (1), 2 (1962), 233–243.Google Scholar
[10]Landau., E.Einige Ungleichungen für zweimal differenzierbare Funktionen. Proc. London Math. Soc. 13 (1913), 43–49.Google Scholar
[11]Lyubich., Yu. I.On the belonging of the powers of an operator on a given vector to a certain linear manifold. Dokl. Akad. Nauk. SSSR 102 (1955), no. 5, 881–884. (Russian.)Google Scholar
[12]Matorin., A. P.Inequalities between the maxima of the absolute values of a function and its derivatives on a half-line. Ukrain. Mat. Zh. 7 (1955), 262–266; Amer. Math. Soc. Translations (2), 8 (1958), 13–17.Google Scholar
[13]Partington., J. R.The resolvent of a Hermitian operator on a Banach space. J. London Math. Soc. (2), 27 (1983), 507–512.Google Scholar
[14]Schoenberg., I. J.The elementary cases of Landau's problem of inequalities between derivatives. Amer. Math. Monthly 80 (1973), 121–158.CrossRefGoogle Scholar
[15]Schoenberg, I. J. and Cavaretta., A.Solution of Landau's problem concerning higher derivatives on the halfline. Proc. Internat. Conf. on Constructive Function Theory, Varna 1970, pp. 297–308. Also in University of Wisconsin MRC Report no. 1050, March 1970.Google Scholar
[16]Stechkin., S. B.Best approximation of linear operators. Mat. Zametki (Math. Notes), 1 (1967), 137–148.Google Scholar
[17]Stechkin., S. B.On the inequalities between the upper bounds of the derivatives of an arbitrary function on the halfline. Mat. Zametki (math. Notes), 1 (1967), 665–674.Google Scholar