Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-09T13:38:34.678Z Has data issue: false hasContentIssue false
  • English
  • Français

Lower algebraic K-theory of certain reflection groups

Published online by Cambridge University Press:  20 November 2009

JEAN-FRANÇOIS LAFONT ,
BRUCE A. MAGURN  and
IVONNE J. ORTIZ
JEAN-FRANÇOIS LAFONT
Affiliation:
Department of Mathematics, Ohio State University, Columbus, OH 43210, U.S.A. e-mail: [email protected]
BRUCE A. MAGURN
Affiliation:
Department of Mathematics, Miami University, Oxford, OH 45056, U.S.A e-mail: [email protected], [email protected]
IVONNE J. ORTIZ
Affiliation:
Department of Mathematics, Miami University, Oxford, OH 45056, U.S.A e-mail: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For P ⊂ 3 a finite volume geodesic polyhedron, with the property that all interior angles between incident faces are of the form π/mij (mij ≥ 2 an integer), there is a naturally associated Coxeter group ΓP. Furthermore, this Coxeter group is a lattice inside the semi-simple Lie group O+(3, 1) = Isom(3), with fundamental domain the original polyhedron P. In this paper, we provide a procedure for computing the lower algebraic K-theory of the integral group ring of such groups ΓP in terms of the geometry of the polyhedron P. As an ingredient in the computation, we explicitly calculate the K−1 and Wh of the groups Dn and Dn × 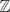3, and we also summarize what is known about the 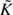0.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 148 , Issue 2 , March 2010 , pp. 193 - 226
Copyright
Copyright © Cambridge Philosophical Society 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[An]Andreev, E. M.Convex polyhedra of finite volume in Lobačevskiĭ space. Math. USSR-Sb. 12 (1970), 255–259.CrossRefGoogle Scholar
[Ba1]Bass, H.The Dirichlet unit theorem, induced characters and Whitehead groups of finite groups. Topology 4 (1965), 391–410.CrossRefGoogle Scholar
[Ba2]Bass, H.Algebraic K-theory (W. A. Benjamin, 1968).Google Scholar
[BFJP]Berkove, E., Farrell, F. T., Juan-Pineda, D. and Pearson, K.The Farrell-Jones isomorphism conjecture for finite covolume hyperbolic actions and the algebraic K-theory of Bianchi groups. Trans. Amer. Math. Soc. 352 (2000), 5689–5702.CrossRefGoogle Scholar
[BB]Bley, W. and Boltje, R. Computation of locally free class groups, in Algorithmic number theory (Lect. Notes in Comput. Sci., 4076), 72–86 (Springer, 2006).CrossRefGoogle Scholar
[C]Carter, D.Lower K-theory of finite groups. Comm. Algebra 8 (1980), 1927–1937.Google Scholar
[CR1]Curtis, C. and Reiner, I.Methods of Representation Theory, Vol. I (John Wiley & Sons, Inc., 1990), xxiv+819 pp.Google Scholar
[CR2]Curtis, C. and Reiner, I.Methods of Representation Theory, Vol. II (John Wiley & Sons, Inc., 1987), xviii+951 pp.Google Scholar
[D]Davis, J. Some remarks on Nil-groups in algebraic K-theory, preprint available at arXiv:0803.1641.Google Scholar
[DKR]Davis, J., Khan, Q. and Ranicki, A. Algebraic K-theory over the infinite dihedral group, preprint available at arXiv:0803.1639.Google Scholar
[DQR]Davis, J., Quinn, F. and Reich, H. Algebraic K-theory of virtually cyclic groups, in preparation.Google Scholar
[Da]Davis, M.The Geometry and Topology of Coxeter Groups (Princeton University Press, 2008), xiv+584 pp.Google Scholar
[De]Deodhar, V. V.On the root system of a Coxeter group. Comm. Algebra 10 (1982), 611–630.CrossRefGoogle Scholar
[EM1]Endó, S. and Miyata, T.On the projective class group of finite groups. Osaka J. Math. 13 (1976), 109–122.Google Scholar
[EM2]Endó, S. and Miyata, T.On the class groups of dihedral groups. J. Algebra 63 (1980), 548–573.Google Scholar
[FJ1]Farrell, F. T. and Jones, L. E.Isomorphism conjectures in algebraic K-theory. J. Amer. Math. Soc. 6 (1993), 249–297.Google Scholar
[FJ2]Farrell, F. T. and Jones, L. E.The lower algebraic K-theory of virtually infinite cyclic groups. K-theory 9 (1995), 13–30.CrossRefGoogle Scholar
[FKW]Fröhlich, A., Keating, M. E. and Wilson, S. M. J.The class groups of quaternion and dihedral 2-groups. Mathematika 21 (1974), 64–71.CrossRefGoogle Scholar
[GRU]Galovich, S., Reiner, I. and Ullom, S.Class groups for integral representations of metacyclic groups. Mathematika 19 (1972), 105–111.Google Scholar
[J]Jacobinski, H.Genera and decompositions of lattices over orders. Acta Math. 121 (1968), 1–29.CrossRefGoogle Scholar
[JKRT]Johnson, N. W., Ratcliffe, J. G., Kellerhals, R. and Tschantz, S. T.The size of a hyperbolic Coxeter simplex. Transform. Groups 4 (1999), 329–353.Google Scholar
[K]Keating, M. E.Class groups of metacyclic groups of order pr q, p a regular prime. Mathematika 21 (1974), 90–95.Google Scholar
[LO1]Lafont, J.-F. and Ortiz, I. J.Relative hyperbolicity, classifying spaces and lower algebraic K-theory. Topology 46 (2007), 527–553.CrossRefGoogle Scholar
[LO2]Lafont, J.-F. and Ortiz, I. J.Lower algebraic K-theory of hyperbolic 3-simplex reflection groups. Comment. Math. Helv. 84 (2009), 297–337.CrossRefGoogle Scholar
[LO3]Lafont, J.-F. and Ortiz, I. J.Relating the Farrell Nil-groups to the Waldhausen Nil-groups. Forum Math. 20 (2008), 445–455.Google Scholar
[Le]Lemmermeyer, F.Ideal class groups of cyclotomic number fields, II. Acta Arith. 84 (1998), 59–70.CrossRefGoogle Scholar
[Li]van der Linden, F. J.Class number computations of real abelian number fields. Math. Comp. 39 (1982), 693–707.CrossRefGoogle Scholar
[Lu]Lück, W.Survey on classifying spaces for families of subgroups, in “Infinite groups: geometric, combinatorial and dynamical aspects”. Progr. Math. 248 (2005), 269–322.Google Scholar
[LR]Lück, W. and Reich, H.The Baum-Connes and the Farrell-Jones conjectures in K- and L-theory, in Handbook of K-theory, Vol. 2, 703–842 (Springer-Verlag, 2005).Google Scholar
[LW]Lück, W. and Weiermann, M. On the classifying space of the family of virtually cyclic subgroups, to appear in Pure Appl. Math. Q.Google Scholar
[Ma1]Magurn, B.SK 1 of dihedral groups. J. Algebra 51 (1978), 399–415. Erratum to SK1 of dihedral groups. J. Algebra 55 (1978), 545–546.Google Scholar
[Ma2]Magurn, B.Whitehead groups of some hyperelementary groups. J. London Math. Soc. 21 (1980), 176–188.CrossRefGoogle Scholar
[Mi]Milnor, J.Whitehead torsion. Bull. Amer. Math. Soc. 72 (1966), 358–426.Google Scholar
[Ol]Oliver, R.Whitehead groups of finite groups. London Math. Soc. Lecture Note Series 132 (Cambridge University Press, 1988), viii+349 pp.CrossRefGoogle Scholar
[OT]Oliver, R. and Taylor, L. R.Logarithmic descriptions of Whitehead groups and class groups for p-groups. Mem. Amer. Math. Soc. 76 (1988), no. 392, vi+97 pp.Google Scholar
[Or]Ortiz, I. J.The lower algebraic K-theory of Γ3. K-theory 32 (2004), 331–355.Google Scholar
[Pe]Pearson, K.Algebraic K-theory of two dimensional crystallographic groups. K-theory 14 (1998), 265–280.Google Scholar
[Qu]Quinn, F.Ends of maps II. Invent. Math. 68 (1982), 353–424.Google Scholar
[R]Ratcliffe, J. G.Foundations of hyperbolic manifolds. Graduate Texts in Mathematics 149 (Springer-Verlag, 1994).Google Scholar
[Re]Reiner, I.Maximal orders. Corrected reprint of the 1975 original. With a foreword by Taylor, M. J.London Math. Soc. Monogra. N. S. 28 (The Clarendon Press, Oxford University Press, 2003), xiv+395 pp.Google Scholar
[RU1]Reiner, I. and Ullom, S. Remarks on class groups of integral group rings, in “Symposia Mathematica. Vol. XIII (Convegno di Gruppi e loro Rappresentazioni, INDAM, Rome, 1972),” 501–516. (Academic Press, 1974).Google Scholar
[RU2]Reiner, I. and Ullom, S.A Mayer-Vietoris sequence for class groups. J. Algebra 31 (1974), 305–342.CrossRefGoogle Scholar
[RHD]Roeder, R. K. W., Hubbard, J. H. and Dunbar, W. D.Andreev's Theorem on hyperbolic polyhedra. Ann. l'Inst. Fourier 57 (2007), 825–882.Google Scholar
[Se1]Serre, J.-P.Local fields. Graduate Texts in Mathematics 67 (Springer-Verlag, 1979), viii+241 pp.CrossRefGoogle Scholar
[Se2]Serre, J.-P.Trees (Springer-Verlag, 1980).Google Scholar
[St]Steinitz, E. Polyeder und Raumeinteilungen in Encyclopädie der mathematischen Wissenschaften Band 3 (Geometrie), Teil 3AB12 (1922), 1–139.Google Scholar
[Sw]Swan, R. G.K-theory of finite groups and orders. Lecture Notes in Math. 149. (Springer-Verlag, 1970), iv+237 pp.Google Scholar
[T]Taylor, M. J.Locally free classgroups of groups of prime power order. J. Algebra 50 (1978), 463–487.Google Scholar
[Wag]Wagstaff, S. S. Jr., The irregular primes to 125000. Math. Comp. 32 (1978), 583–591.Google Scholar
[Wa]Wall, C. T. C.Norms of units in group rings. Proc. London Math. Soc. 29 (1974), 593–632.Google Scholar
[Wd]Waldhausen, F.Algebraic K-theory of generalized free product I, II. Ann. of Math. 108 (1978), 135–256.Google Scholar
[Wh]Whitney, H.Congruent graphs and the connectivity of graphs. Ameri. J. Math. 54 (1932), 150–168.CrossRefGoogle Scholar
[We]Weibel, C.NK 0 and NK 1 of the groups C 4 and D 4. Comment. Math. Helv. 84 (2009), 339–349.Google Scholar
[Z]Ziegler, G. M.Lectures on polytopes. Graduate Texts in Mathematics 152 (Springer-Verlag, 1995), ix+370 pp.Google Scholar