Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T14:25:37.797Z Has data issue: false hasContentIssue false
  • English
  • Français

Locally free (ℙn)-modules

Published online by Cambridge University Press:  24 October 2008

S. C. Coutinho  and
M. P. Holland
S. C. Coutinho
Affiliation:
Instituto de Matematica, Universidade Federal do Rio de Janeiro, Brazil
M. P. Holland
Affiliation:
Department of Pure Mathematics, Sheffield University, Sheffield S3 7RH
Get access Rights & Permissions [Opens in a new window]

Extract

The purpose of this paper is to study the structure of locally free modules over the ring of differential operators on projective space. Let 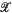be a non-singular, complex, algebraic variety. Denote by 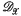the sheaf of rings of differential operators over 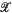and by 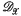its ring of global sections. A 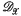-module M is called locally free if the associated sheaf 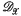⊗ M is locally free as a sheaf of 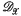-modules. Locally free modules arise naturally in -module theory as inverse images of determined modules; see [1] for definitions and examples.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 112 , Issue 2 , September 1992 , pp. 233 - 245
Copyright
Copyright © Cambridge Philosophical Society 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Andronikof, E.. Systèmes déterminés et systèmes normaux d'équations aux dérivées partielles. C. R. Acad. Sci. Paris Sér. I Math. 293 (1981), 257–260.Google Scholar
[2]Bass, H.. Finitistic dimension and a homological generalisation of semiprimary rings. Trans. Amer. Math. Soc. 95 (1960), 466–488.CrossRefGoogle Scholar
[3]Beilinson, A. and Bernstein, J.. Localisation de g-modules. C. R. Acad. Sci. Paris Sér. I Math. 292 (1981), 15–18.Google Scholar
[4]Coutinho, S. C.. Basic element theory of noncommutative Noetherian rings. J. Algebra 144 (1991), 24–42.CrossRefGoogle Scholar
[5]Coutinho, S. C. and Holland, M. P.. Differential operators on smooth varieties. In Séminaire d'Algèbra Malliavin, Lecture notes in Math. vol. 1404 (Springer-Verlag, 1989), pp. 201–219.CrossRefGoogle Scholar
[6]Coutinho, S. C. and Holland, M. P.. K-theory of twisted differential operators. J. London Math. Soc. (2), to appear.Google Scholar
[7]Grothendieck, A.. Sur Ia classification des fibres holomorphes sur la sphére de Riemann. Amer. J. Math. 79 (1957), 121–138.CrossRefGoogle Scholar
[8]Hartshorne, R.. Algebraic Geometry. Graduate Texts in Math. vol. 52 (Springer-Verlag, 1977).CrossRefGoogle Scholar
[9]Hodges, T. J.. K-theory of D-modules and primitive factors of enveloping algebras of semisimple Lie algebras. Bull. Sci. Math. (2) 113 (1989), 85–88.Google Scholar
[10]Holland, M. P. and Stafford, J. T.. Differential operators on rational projective curves. J. Algebra 147 (1992), 176–244.CrossRefGoogle Scholar
[11]Magurn, B. A., Van Der Kallen, W. and Vaserstein, L. N.. Absolute stable rank and Witt cancellation for non-commutative rings. Invent. Math. 911 (1988), 525–542.CrossRefGoogle Scholar
[12]Okonek, C., Schneider, M. and Spindler, H.. Vector Bundles on Complex Projective Spaces, Progress in Math. no. 3 (Birkhäuser, 1980).Google Scholar
[13]Stafford, J. T.. Module structure of Weyl algebras. J. London Math. Soc. (2) 18 (1977), 429–442.Google Scholar
[14]Stafford, J. T.. Generating modules efficiently: algebraic K-theory for noncommutative Noetherian rings. J. Algebra 69 (1981), 312–346.CrossRefGoogle Scholar
[15]Stafford, J. T.. Homological properties of the enveloping algebra U(SL 2). Math. Proc. Cambridge Philos. Soc. 91 (1982), 29–37.CrossRefGoogle Scholar
[16]Stafford, J. T.. Stably free, projective right ideals. Compositio Math. 54 (1985), 63–78.Google Scholar
[17]Stafford, J. T.. Endomorphisms of right ideals of the Weyl algebra. Trans. Amer. Math. Soc. 299 (1987), 623–639.CrossRefGoogle Scholar