Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-29T18:20:15.893Z Has data issue: false hasContentIssue false
  • English
  • Français

Localization of stable homotopy rings

Published online by Cambridge University Press:  24 October 2008

R. D. Arthan
R. D. Arthan
Affiliation:
Queen Mary College, London
Get access Rights & Permissions [Opens in a new window]

Extract

V. P. Snaith has shown that a number of interesting homology theories (e.g. K-theory, complex cobordism) arise when one localizes the stable homotopy type of certain H-spaces (BU(1), BU, etc.). In this paper we sketch a construction which, given an H-space X and 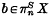, produces a ring spectrum IΣ−nX which lies between Xand its localization with respect to b, and in many cases has a tractable structure. We apply this when X is an Eilenberg-MacLane space K(ℤ/, n) and 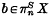is a generator (p = 0 or a prime), and get complete results on the localizations in this case. The results confirm one's suspicions that localization is a fairly drastic manoeuvre, cutting down the large and complicated ring 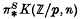to something more or less trivial, except when p = 0 and n = 2, in which case the rich geometry of K(ℤ, 2) = BU(1) gives complex K-theory.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 93 , Issue 2 , March 1983 , pp. 295 - 302
Copyright
Copyright © Cambridge Philosophical Society 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Adams, J. F.Stable homotopy and generalised homology. (University of Chicago Press, 1974.)Google Scholar
(2)Arthan, R. D. Thesis. (London University, 1982.)Google Scholar
(3)Browder, W., Liulevicius, A. and Peterson, F. P.Cobordism theories. Ann. of Math. 84 (1965), 91–101.CrossRefGoogle Scholar
(4)Johnson, D. C. and Wilson, W. S.Projective dimension and Brown-Peterson homology. Topology 12 (1973), 327–353.CrossRefGoogle Scholar
(5)Mosher, R. E.Some stable homotopy of complex projective space. Topology 7 (1968), 179–193.CrossRefGoogle Scholar
(6)Peterson, F. P.Coalgebras over Hopf algebras. Lecture Notes in Mathematics, no. 168 (1970), 246–249.Google Scholar
(7)Robinson, A. Derived tensor products of module spectra. To appear.Google Scholar
(8)Snaith, V. P.Algebraic cobordism and K-theory. Mem. Amer. Math. Soc. 221 (1979).Google Scholar
(9)Snaith, V. P.Localised stable homotopy of some classifying spaces. Proc. Cambridge Philos. Soc. 89 (1981), 325–330.CrossRefGoogle Scholar
(10)Steenrod, N. and Epstein, D. B. A.Cohomology operations. Ann. Math. Studies 50 (Princeton University Press, 1968).Google Scholar