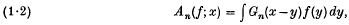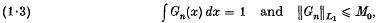Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ditzian, Z.
1984.
Functional Analysis, Holomorphy and Approximation Theory II.
Vol. 86,
Issue. ,
p.
57.
Ditzian, Z.
1986.
On divided differences onC[a, b], L p [a, b] and other spaces.
Periodica Mathematica Hungarica,
Vol. 17,
Issue. 1,
p.
45.
Singh, Mradul Veer
Mittal, ML
and
Rhoades, BE
2017.
Approximation of functions in the generalized Zygmund class using Hausdorff means.
Journal of Inequalities and Applications,
Vol. 2017,
Issue. 1,


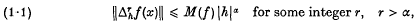
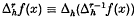 and Δ
and Δ