Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T14:54:03.471Z Has data issue: false hasContentIssue false
  • English
  • Français

Lifting amalgamated sums and other colimits of groups and topological groups

Published online by Cambridge University Press:  24 October 2008

Ronald Brown  and
Philip R. Heath
Ronald Brown
Affiliation:
Department of Pure Mathematics, University College of North Wales, Bangor, Gwynedd LL57 2UW
Philip R. Heath
Affiliation:
Department of Mathematics, Memorial University of Newfoundland, St John's, Newfoundland A1C 5S7, Canada
Get access Rights & Permissions [Opens in a new window]

Extract

Suppose a group H is given as a free product with amalgamation

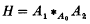
determined by groups A0, A1, A2 and homomorphisms α1: A0 → A1, α2: A0 → A2. Thus H may be described as the quotient of the free product A * A2 by the relations i1 α1 (α0) = i2α2 (α0) for all α0 ∈ A0, where i1, i2 are the two injections of A1, A2 into A1 * A2. We do not assume that α1, α2 are injective, so the canonical homomorphisms α′i: Ai → H, i = 0,1,2, also need not be injective.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 102 , Issue 2 , September 1987 , pp. 273 - 280
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Booth, P. I. and Brown, R.. Spaces of partial maps, fibred mapping spaces and the compactopen topology. Gen. Top. Appl. 8 (1978), 181–195.CrossRefGoogle Scholar
[2]Brown, R.. Fibrations of groupoids. J. Algebra 15 (1970), 103–132.CrossRefGoogle Scholar
[3]Brown, R.. Some nonprojective subgroups of free topological groups. Proc. Amer. Math. Soc. 52 (1975), 433–440.CrossRefGoogle Scholar
[4]Brown, R. and Nicholas, P.. Exponential laws for topological categories, groupoids and groups, and mapping spaces of colimits. Cah. Top. Géom. Diff. 20 (1979), 179–198.Google Scholar
[5]Conduché, F.. Au sujet de l'existence d'adjoints à droite aux foncteurs image réciproque dans la catégorie des catégories. C.R.A.S. Paris 275 A (1972), 891–894.Google Scholar
[6]Higgins, P. J.. Notes on Categories and Groupoids (Van Nostrand, 1971).Google Scholar
[7]Howie, J.. Pullback functors and crossed complexes. Cah. Top. Géom. Diff. 20 (1979), 281–296.Google Scholar
[8]LaMartin, W. F.. On the foundations of k-group theory. Diss. Math. (Rozprawy Mat.) 146 (1977).Google Scholar
[9]Mac Lane, S.. Categories for the Working Mathematician (Springer-Verlag, 1971).CrossRefGoogle Scholar
[10]Nickolas, P.. Free products of k ω-topological groups with a closed subgroup amalgamated. J. Austral. Math. Soc. (Series A) 40 (1986), 414–420.CrossRefGoogle Scholar