Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-29T18:58:14.697Z Has data issue: false hasContentIssue false
  • English
  • Français

The Lebesgue-Stieltjes Integral

Published online by Cambridge University Press:  24 October 2008

E. C. Francis
E. C. Francis
Affiliation:
Peterhouse
Get access Rights & Permissions [Opens in a new window]

Extract

It has long been realized that a Stieltjes integral can be defined and developed on the same lines as a Lebesgue integral, using in place of the measure of a set E the variation of an increasing function ø (x) upon E; but only the more obvious—and less useful—properties of such an integral seem to have been stated. The original integral defined by Stieltjes possesses the remarkable Integration by Parts property that if either of 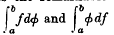exists, so does the other, and their sum is equal to

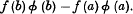
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 22 , Issue 6 , November 1925 , pp. 935 - 950
Copyright
Copyright © Cambridge Philosophical Society 1925

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Stieltjes, T. J., “Recherches sur les Fractions Continues,” Ann. de la Fac. des Sc. de, Toulouse, vol. VIII (1894).Google Scholar

† E.g. Young, W. H., “Integration with respect to a Function of Bounded Variation,” Proc. L. M. S. vol. XIII (1913)Google Scholar, proves that if u and v are positive increasing functions such that both u has an RS (Riemann-Stieltjes) integral with respect to u and u with respect to u, then

where the constant is zero if either function is continuous.

† The Integration by Parts theorem proved in this paper has also been given—proved by quite different methods—by Danniell, P. J., “On differentiation with regard to a function of limited variation,” Trans. Amer. Math. Soc. vol. xix, p. 353 (1918).CrossRefGoogle Scholar

§ Francis, E. C., “On Differentiation with respect to a Function,” Proc. Camb. Phil. Soc. vol. 22, p. 924.CrossRefGoogle Scholar

* Pollard, S., “The Stieltjes Integral and its Generalizations,” Q. J. vol. XLIX 1920–1921.Google Scholar

† Young, W. H., “On the general theory of integration,” Phil. Trans. R. S. (A), 204, pp. 221–252 (1904).CrossRefGoogle Scholar

* Francis, E. C., loc. cit.Google Scholar

† E. C. Francis, ibid.

‡ I.e. measurable with respect to ø.Google Scholar

* When ø (x) is continuous we have seen that the LS-integral is continuous. It is therefore possible to revert to the simpler notation LS in place of LS Google Scholar

* Lebesgue, Leçons sur l' intégration, p. 58.Google Scholar

* We have supposed f (x), ø (x) increasing. For other cases the modification required is obvious.Google Scholar

* Francis, E. C., loc. cit.Google Scholar

* Francis, E. C., loc. cit.Google Scholar

* If ψ(x) is not positive we can express it as the difference of two positive functions ψ1(x), ψ2 (x). f (x) ψ1 (x), f (x) ψ2 (x) are measurable ø and it is easily seen that the existence of and therefore of follows at once from that of .Google Scholar