Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-30T22:33:42.936Z Has data issue: false hasContentIssue false
  • English
  • Français

The least limit point of the spectrum associated with sinǵular differential operators

Published online by Cambridge University Press:  24 October 2008

M. S. P. Eastham
M. S. P. Eastham
Affiliation:
The University, Southampton
Get access Rights & Permissions [Opens in a new window]

Extract

Let τ be the formally self-adjoint differential operator denned by

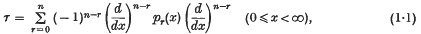
where the pr(x) are real-valued, 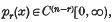, and p0(x) > 0. Then τ determines a real symmetric linear operator T0, given by T0f = τf, whose domain D(T0) consists of those functions f in the complex space L2(0, ∞) which have compact support and 2n continuous derivatives in (0, ∞) and vanish in some right neighbourhood of x = 0 ((7), p. 27–8). Since D(T0) is dense in L2(0, ∞), T0 has a self-adjoint extension T. We denote by μ the least limit point of the spectrum of T. The operator T may not be unique, but all such T have the same essential spectrum ((7), p. 28) and therefore μ does not depend on the choice of T.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 67 , Issue 2 , March 1970 , pp. 277 - 281
Copyright
Copyright © Cambridge Philosophical Society 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Balslev, E.The singular spectrum of elliptic differential operators in L p(R n). Math. Scand. 19 (1966), 193–210.CrossRefGoogle Scholar
(2)Coddington, E. A. and Levinson, N.Theory of ordinary differential equations (McGraw-Hill, 1955).Google Scholar
(3)Eastham, M. S. P.On the limit points of the spectrum J. London Math. Soc. 43 (1968), 253–260.CrossRefGoogle Scholar
(4)Eastham, M. S. P.Gaps in the essential spectrum associated with singular differential operators. Quart. J. Math. Oxford Ser. 18 (1967), 155–168.CrossRefGoogle Scholar
(5)Everitt, W. N.Singular differential equations I: the even order case. Math. Ann. 156 (1964), 9–24.CrossRefGoogle Scholar
(6)Everitt, W. N.Singular differential equations II; some self-adjoint even order cases. Quart. J. Math. Oxford Ser. 18 (1967), 13–32.CrossRefGoogle Scholar
(7)Glazman, I. M.Direct methods of qualitative spectral analysis of singular differential operators (I.P.S.T., Jerusalem, 1965).Google Scholar
(8)Goldberg, S.Unbounded linear operators (McGraw-Hill, 1966).Google Scholar
(9)Hartman, P. and Putnam, C. R.The least cluster point of the spectrum of boundary value problems. Amer. J. Math. 70 (1948), 849–855.CrossRefGoogle Scholar
(10)Titchmarsh, E. C.Eigenfunction expansions, part 1 (2nd ed., Oxford, 1962).Google Scholar
(11)Wood, A. D. Dundee Ph.D. thesis, 1968.Google Scholar