Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-23T11:34:31.686Z Has data issue: false hasContentIssue false
  • English
  • Français

The lattice properties of asymmetric hyperbolic regions

II. On a theorem of davenport

Published online by Cambridge University Press:  24 October 2008

J. W. S. Cassels
J. W. S. Cassels
Affiliation:
Trinity CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper, all numbers are real and all radicals are positive.

Let f(x, y) = ax2 + bxy + cy2 be an indefinite quadratic form, and let d = Δ2 = b2 − 4ac, where Δ > 0. A well-known theorem of Minkowski states that, if (x0, y0) is any pair of numbers, then there exists a pair (x, y), x ≡ x0 (mod 1), y ≡ y0 (mod 1), say (x, y) ≡ (x0, y0) (mod 1), such that

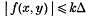
for k ≥ ¼, and Davenport has shown how this result may be improved if we know a value assumed by f(x, y) for coprime integral values, (x, y) = (m, n) ≠ (0, 0). In this paper, we discuss the more general inequality

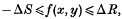
where R and S are constants, and use the method developed in the first paper of this series to obtain a sharper and more general theorem than Davenport's. We give an application to the theory of real Euclidean quadratic fields and to a problem in Diophantine approximation discussed by Khintchine.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 44 , Issue 2 , April 1948 , pp. 145 - 154
Copyright
Copyright © Cambridge Philosophical Society 1948

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

† Davenport, , Proc. K. Akad. Wet. Amsterdam, 49 (1946), 815–21.Google Scholar This paper used elementary methods. In two subsequent papers, ibid. 50 (1947), 378–89 and 484–91, Prof. Davenport uses deeper methods to discuss completely x 2 + xy − y 2 and 5x 2 + 11xy − 5y 2.

‡ Cassels, , Proc. Cambridge Phil. Soc. 44 (1948), 1–7.CrossRefGoogle Scholar

§ Khintchine, , Bull. Acad. Sci. U.R.S.S. 10 (1946), 281–93.Google Scholar

∥ For a definition of the lattice-theoretic terms employed, see my earlier paper.

† See Fig. 1.

‡ In this and later applications of the lemma, the points A, B, C, D do not necessarily correspond to the points so named in the enunciation of the lemma. Here, for instance, A, B, Ā correspond to A, B, C, D respectively in the lemma.

† See Fig. 2.

‡ See Fig. 3.

† In the wide sense, i.e., of determinant ± 1.

‡ As I know of no reference to exactly what is required, I sketch a proof from first principles: As (X 1, Y 1) ≠ (0, 0), at least one of the two transformations

is non-degenerate, and the transform (X′1, Y′1) of (X 1, Y 1) lies in either case on the X′-axis (i.e. X′1 ≠ Y′1 = 0). We assume T non-degenerate, and write

If f(X 1, Y 1) = f′(X′1, 0) = 0, then a′ = 0, but, as Δ ≠ 0, necessarily b′ ≠ 0. Hence f(X, Y) = X″ Y″ where the transformation

is non-degenerate, and the ambiguous sign is such that X″1 > 0 (with the obvious meaning for X″1). If, however, f(X 1, Y 1) = f′(X′1, 0) > 0, then a′ > 0 and

where b′2 − 4a′c′ > 0. The transformation

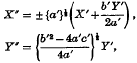
is real and non-degenerate, and the ambiguous sign may be taken so that X″1 > 0. Hence

If f(X, Y 1) < 0, we put − f(X, Y) for f(X, Y) in the foregoing analysis. In any case, we now write

where, as (X″, Y″) is connected to (X, Y) by a chain of non-degenerate linear substitutions, we may choose ρ > 0 so that the substitution linking x, y to X, Y is unimodular. Finally, the numerical coefficient in the expressions Δxy and ½Δ(x2 − y2) is a consequence of the well-known invariance of the discriminant under unimodular substitution.

† That is, the covariant 2amμ + b(mν + μn) + 2cnν vanishes.

† For there exists an integer M such that Mf(X, Y) = F(X, Y) has integral coefficients and so, by Landau, Vorlesungen (Leipzig, 1927) Satz 202 (vol. 1, p. 139), has an infinity of automorphisms. We take for (m 1, n 1) the image of (m, n) under any automorphism.

‡ Loc. cit. in § 1.

§ Loc. cit.

† And also for t = 19, 57, 73 and 97; but this is more difficult. It is not known if this is all, but any more values of t must be primes congruent to 1 (mod 24). See Redei, L., Math. Ann. 118 (1942), 588–608CrossRefGoogle Scholar, which has an almost complete list of references. For an elementary account of the Euclidean Algorithm see Hardy, G. H. and Wright, E. M., Introduction to the Theory of Numbers (Oxford, 1938)Google Scholar, § 14·8.

† If (a, b) and (c, d) are two points and (A, B), (C, D) their respective transforms under unimodular transformation, then

To obtain (12) from Lemma 2 write

(a, b) = (x, y), (A, B) = (x k, y k), (c, d) = (ξ, 0) and (C, D) = (m k, n k).

† Loc. cit. § 1.

‡ Cassels, loc. cit.

§ Davenport, H. and Heilbronn, H., 'On asymmetric inequalities for the product of two non-homogeneous linear forms', J. London Math. Soc. 22 (1947), 53–61.CrossRefGoogle Scholar I am grateful to Prof. Davenport for telling me of this paper, and also for pointing out the paper by Khintchine.