Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bartel, Alex
2012.
On Brauer–Kuroda type relations of S-class numbers in dihedral extensions.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2012,
Issue. 668,
Česnavičius, Kęstutis
2017.
p-Selmer growth in extensions of degree p.
Journal of the London Mathematical Society,
Vol. 95,
Issue. 3,
p.
833.
Dokchitser, Vladimir
Evans, Robert
and
Wiersema, Hanneke
2021.
On a BSD-type formula for L-values of Artin twists of elliptic curves.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2021,
Issue. 773,
p.
199.


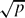 ) if
) if 