Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-20T00:44:47.255Z Has data issue: false hasContentIssue false
  • English
  • Français

Large deviations of the limiting distribution in the Shanks–Rényi prime number race

Published online by Cambridge University Press:  28 February 2012

YOUNESS LAMZOURI
YOUNESS LAMZOURI*
Affiliation:
Department of Mathematics, University of Illinois at Urbana–Champaign, 1409 W. Green Street, Urbana, IL, 61801, U.S.A. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let q ≥ 3, 2 ≤ r ≤ φ(q) and a1, . . ., ar be distinct residue classes modulo q that are relatively prime to q. Assuming the Generalized Riemann Hypothesis (GRH) and the Linear Independence Hypothesis (LI), M. Rubinstein and P. Sarnak [11] showed that the vector-valued function Eq;a1, . . ., ar(x) = (E(x;q,a1), . . ., E(x;q,ar)), where 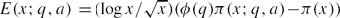, has a limiting distribution μq;a1, . . ., ar which is absolutely continuous on . Furthermore, they proved that for r fixed, μq;a1, . . ., ar tends to a multidimensional Gaussian as q → ∞. In the present paper, we determine the exact rate of this convergence, and investigate the asymptotic behavior of the large deviations of μq;a1, . . ., ar.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 153 , Issue 1 , July 2012 , pp. 147 - 166
Copyright
Copyright © Cambridge Philosophical Society 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Davenport, H.Multiplicative number theory. Graduate Texts in Mathematics, 74 (Springer-Verlag, New York, 2000).Google Scholar
[2]Fiorilli, D. and Martin, G. Inequities in the Shanks–Rényi prime number race: an asymptotic formula for the densities. To appear in J. Reine Angew. Math.Google Scholar
[3]Knapowski, S. and Turán, P.Comparative prime-number theory. I. Acta Math. Acad. Sci. Hungar. 13 (1962), 299–314; II. 13 (1962), 315–342; III. 13 (1962), 343–364; IV. 14 (1963), 31–42; V. 14 (1963), 43–63; VI. 14 (1963), 65–78; VII. 14 (1963), 241–250; VIII. 14 (1963), 251–268.CrossRefGoogle Scholar
[4]Kaczorowski, J.A contribution to the Shanks–Rényi race problem. Quart. J. Math. Oxford Ser. (2) 44 (1993), no. 176, 451–458.CrossRefGoogle Scholar
[5]Kaczorowski, J.On the Shanks–Rényi race problem. Acta Arith. 74 (1996), no. 1, 31–46.CrossRefGoogle Scholar
[6]Lamzouri, Y.Prime number races with three or more competitors, 38 pages. ArXiv:1101.0836.Google Scholar
[7]Littlewood, J. E.On the class number of the corpus . Proc. London Math. Soc. 27 (1928), 358–372.CrossRefGoogle Scholar
[8]Monach, W. R. Numerical investigation of several problems in number theory. Ph.D Dissertation University of Michigan (1980).Google Scholar
[9]Montgomery, H. L.The zeta function and prime numbers. Proceedings of the Queen's Number Theory Conference, 1979 (Kingston, Ontario University), pp. 14–24, Queen's Papers in Pure and Appl. Math. 54 (Queen's Kingston, 1980).Google Scholar
[10]Montgomery, H. L. and Odlyzko, A. M.Large deviations of sums of independent random variables. Acta Arith. 49 (1988), no. 4, 427–434.CrossRefGoogle Scholar
[11]Rubinstein, M. and Sarnak, P.Chebyshev's bias. Experiment. Math. 3 (1994), no. 3, 173–197.CrossRefGoogle Scholar