Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T13:30:05.988Z Has data issue: false hasContentIssue false
  • English
  • Français

Large correlated families of positive random variables

Published online by Cambridge University Press:  24 October 2008

D. H. Fremlin
D. H. Fremlin
Affiliation:
University of Essex, Colchester, England
Get access Rights & Permissions [Opens in a new window]

Extract

S. Argyros and N. Kalamidas([l], repeated in [2], Theorem 6·15) proved the following. If κ is a cardinal of uncountable cofinality, and 〈Eξ〉ξ<κ is a family of measurable sets in a probability space (X, μ) such that infξ<κμEξ = δ, and if n ≥ 1, 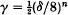, then there is a set Γ ⊆ κ such that #(Γ) = κ and μ(∩ξ∈IEξ) ≥ γ whenever I ⊆ ξ has n members. In Proposition 7 below I refine this result by (i) taking any γ < δn (which is best possible) and (ii) extending the result to infinite cardinals of countable cofinality, thereby removing what turns out to be an irrelevant restriction. The proof makes it natural to perform a further extension to general uniformly bounded families of non-negative measurable functions in place of characteristic functions.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 103 , Issue 1 , January 1988 , pp. 147 - 162
Copyright
Copyright © Cambridge Philosophical Society 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Argyros, S. A. and Kalamidas, N.. The k αn property on spaces with strictly positive measures. Canad. J. Math. 34 (1982), 1047–1058.CrossRefGoogle Scholar
[2]Comfort, W. W. and Negrepontis, S.. Chain Conditions in Topology (Cambridge University Press, 1982).CrossRefGoogle Scholar
[3]Dunford, N. and Schwartz, J. T.. Linear Operators I (Interscience, 1958).Google Scholar
[4]Erdös, P., Hajnal, A., Maté, A. and Rado, R.. Combinatorial Set Theory: Partition Relations for Cardinals (Akademiai Kiado, Budapest, 1984).Google Scholar
[5]Fremlin, D. H.. Topological Riesz Spaces and Measure Theory (Cambridge University Press, 1974).CrossRefGoogle Scholar
[6]Fremlin, D. H.. Consequences of Martin's Axiom (Cambridge University Press, 1984).CrossRefGoogle Scholar
[7]Fremlin, D. H.. Measure algebras. In Handbook of Boolean Algebra (ed. Monk, J. D.) (North-Holland, in preparation).Google Scholar
[8]Hardy, G. H., Littlewood, J. E. and Pólya, G.. Inequalities (Cambridge University Press, 1934).Google Scholar