Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T14:05:17.808Z Has data issue: false hasContentIssue false
  • English
  • Français

La conjecture de Manin pour une famille de variétés en dimension supérieure

Published online by Cambridge University Press:  29 April 2018

KEVIN DESTAGNOL
KEVIN DESTAGNOL*
Affiliation:
Institut de Mathématiques de Jussieu-Paris Rive Gauche, UMR 7586, Université Paris Diderot-Paris 7, Case postale 6052, Bâtiment Sophie Germain, 75205, Paris Cedex 13, France. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Inspired by a method of La Bretèche relying on some unique factorisation, we generalise work of Blomer, Brüdern and Salberger to prove Manin's conjecture in its strong form conjectured by Peyre for some infinite family of varieties of higher dimension. The varieties under consideration in this paper correspond to the singular projective varieties defined by the following equation

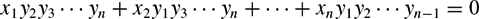$$ x_1 y_2y_3\cdots y_n+x_2y_1y_3 \cdots y_n+ \cdots+x_n y_1 y_2 \cdots y_{n-1}=0 $$
in ℙℚ2n−1 for all n ⩾ 3. This paper comes with an Appendix by Per Salberger constructing a crepant resolution of the above varieties.

En s'inspirant d'une méthode due à La Bretèche reposant sur une factorisation unique, nous généralisons des travaux récents de Blomer, Brüdern, et Salberger en établissant la conjecture de Manin sous sa forme forte conjecturée par Peyre pour une famille infinie de variétés en dimension supérieure. Les variétés considérées dans cet article correspondent aux variétés projectives singulières définies par l'équation suivante

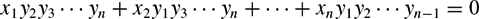$$ x_1 y_2y_3\cdots y_n+x_2y_1y_3 \cdots y_n+ \cdots+x_n y_1 y_2 \cdots y_{n-1}=0 $$
dans ℙℚ2n−1 pour tout n ⩾ 3. Cet article est accompagné d'une Annexe de Per Salberger dans laquelle une résolution crépante des variétés ci-dessus est explicitée.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 166 , Issue 3 , May 2019 , pp. 433 - 486
Copyright
Copyright © Cambridge Philosophical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

RÉFÉRENCES

[1] Batyrev, V. et Tschinkel, Y. Manin's conjecture for toric varieties. J. Algebraic Geom. 7 (1998), 15–53.Google Scholar
[2] Blomer, V. et Brüdern, J. The density of rational points on a certain threefold. Contribution to analytic and algebraic number theory. Springer Proceedings in Mathematics 9 (eds Blomer, V. and Mihailescu, P.) (2016), 1–15.Google Scholar
[3] Blomer, V., Brüdern, J. et Salberger, P. On a certain senary cubic form. Proc. London Math. Soc. 108 (2014), 911–964.10.1112/plms/pdt043Google Scholar
[4] Blomer, V., Brüdern, J. et Salberger, P. The Manin–Peyre conjecture for a certain biprojective cubic threefold. Preprint arXiv:1609.02837 https://arxiv.org/pdf/1609.02837v1.pdf (2016).Google Scholar
[5] Le Boudec, P. Manin's conjecture for two quartic del Pezzo surfaces with 3A 1 and A 1 + A 2 singularity types. Acta Arithmetica 151 (2016), 109–163.10.4064/aa151-2-1Google Scholar
[6] Bourqui, D. Fonction zêta des hauteurs des variétés toriques non déployées. Mem. Amer. Math. Soc. vol. 211. (American Mathematical Society, 2011.)10.1090/S0065-9266-2010-00609-4Google Scholar
[7] de la Bretèche, R. Sur le nombre de matrices aléatoires à coefficients rationnels. À paraître (2016).Google Scholar
[8] de la Bretèche, R. et Tenenbaum, G. Sur les processus arithmétiques liés aux diviseurs. Adv. Appl. Prob., Spec. vol. 48A (2016), (volume en l'honneur de Bingham).Google Scholar
[9] Chambert–Loir, A. et Tschinkel, Y. On the distribution of points of bounded height on equivariant compactifications of vector groups. Invent. Math. 148 (2002), 421–452.10.1007/s002220100200Google Scholar
[10] Colliot–Thélène, J.–L. et Sansuc, J.–J. La descente sur les variétés rationnelles, II. Duke Math. J. 54 (1987), 375–492.10.1215/S0012-7094-87-05420-2Google Scholar
[11] De Concini, C. et Procesi, C. Wonderful models of subspace arrangements. Selecta Math. (N.S.) 1 (1995), 459–494.10.1007/BF01589496Google Scholar
[12] Cox, D.A. The homogeneous coordinate ring of a toric variety. J. Alg. Geom. 4 (1995), 17–50.Google Scholar
[13] Franke, J., Manin, Y. et Tschinkel, Y. Rational points on bounded height on Fano varieties. Inv. Math. J. 54 (1987), 375–492.Google Scholar
[14] Fulton, W. Introduction to Toric Varieties. Annals of Math. Stud. (Princeton University Press, 1993).Google Scholar
[15] Griffiths, P. et Harrus, J. Principles of Algebraic Geometry (Wiley, New York, 1978).Google Scholar
[16] Grothendieck, A. éléments de géométrie algébrique (rédigés avec la collaboration de Jean Dieudonné) : IV. étude locale des schémas et des morphismes de schémas, Quatrième partie. Publ. Math. 'IHéS 32 (1967), 361 pp.Google Scholar
[17] Grothendieck, A. Le groupe de Brauer, III. Exemples et compléments. Dix exposés sur la cohomologie des schémas Adv. Stud. Pure Math. 3 North Holland publishing Company, 11 (1968), 88–188.Google Scholar
[18] Hall, R. R Sets of multiples. Cambridge Tracts in Mathematics 118. (Cambridge University Press, Cambridge, 1996).Google Scholar
[19] Hartshorne, R. Algebraic geometry. Graduate Texts in Math. 52 (Springer, Berlin, 1977), (2008).Google Scholar
[20] Henderson, A. Rational cohomology of the real Coxeter toric variety of type A. Preprint https://arxiv.org/pdf/1011.3860v1.pdf (2010).Google Scholar
[21] Milne, J.S. étale cohomology (Princeton University Press, Princeton, NJ, 1980).Google Scholar
[22] Peyre, E. Hauteurs et mesures de Tamagawa sur les variétés de Fano. Duke Math. J. 79 (1995), 101–218.10.1215/S0012-7094-95-07904-6Google Scholar
[23] Peyre, E. Points de hauteur bornée, topologie adélique et mesures de Tamagawa. J. Théor. Nombres Bordeaux 15 (2003), 319–349. Les XXIIèmes Journées Arithmétiques (Lilles, 2001).10.5802/jtnb.405Google Scholar
[24] Reid, M. Chapter on algebraic surfaces. Complex algebraic varieties, IAS/Park City Math. Series 3 (Éd. J.Kollar) (American Mathematical Society, Providence, RI, 1997).10.1090/pcms/003/02Google Scholar
[25] Salberger, P. Tamagawa numbers of universal torsors and points of bounded height on Fano varieties. Nombre et répartition de points de hauteur bornée. Astérisque 251 (1998), 91–258.Google Scholar
[26] Shparlinski, I. Linear equations with rational fractions of bounded height and stochastic matrices. À paraître au Quart. J. Math. (2016).Google Scholar
[27] Skorobogatov, A. Torsors and Rational Points, volume 16 (Cambridge Univ. Press, Cambridge, 2001).10.1017/CBO9780511549588Google Scholar
[28] Stembridge, J. R. Eulerian numbers, tableaux, and the Betti variety of a toric variety. Discrete Mathematics 99 North Holland, (1992), 302–320.10.1016/0012-365X(92)90378-SGoogle Scholar
[29] Tanimoto, S. et Tschinkel, Y. Height zeta functions of equivariant compactifications of semi-direct products of algebraic groups. Contemp. Math. 566 (2012), 119–157.10.1090/conm/566/11218Google Scholar
[30] Tenenbaum, G. Introduction à la Théorie Analytique et Probabiliste des Nombres. Troisième édition, coll. (Échelles, Belin, 2008), 592 pp.Google Scholar