Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T13:52:21.395Z Has data issue: false hasContentIssue false
  • English
  • Français

Kernels with only a finite number of characteristic values

Published online by Cambridge University Press:  24 October 2008

Dale W. Swann
Dale W. Swann
Affiliation:
Bell Telephone Laboratories, Incorporated, Whippany, New Jersey, 07981
Get access Rights & Permissions [Opens in a new window]

Extract

Let K(s, t) be a complex-valued L2 kernel on the square ⋜ s, t ⋜ by which we mean

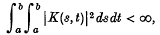
and let {λν}, perhaps empty, be the set of finite characteristic values (f.c.v.) of K(s, t), i.e. complex numbers with which there are associated non-trivial L2 functions øν(s) satisfying

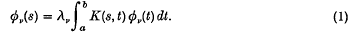
For such kernels, the iterated kernels,

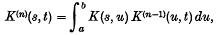
are well-defined (1), as are the higher order traces

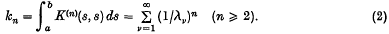
Carleman(2) showed that the f.c.v. of K are the zeros of the modified Fredhoim determinant

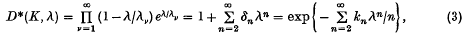
the latter expression holding only for |λ| sufficiently small (3). The δn in (3) may be calculated, at least in theory, by well-known formulae involving the higher order traces (1). For our later analysis of this case, we define 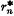and 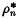, respectively, as the minimum and maximum moduli of the zeros of 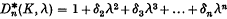, the nth section of D*(K, λ).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 70 , Issue 2 , September 1971 , pp. 257 - 262
Copyright
Copyright © Cambridge Philosophical Society 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Smithies, F.Integral equations. Cambridge Tracts, No. 49 (Cambridge University Press, London, 1958).Google Scholar
(2)Carleman, T.Zur Theorie der linearen Integraigleichungen. Math. Zeit. 9 (1921), 196–217.CrossRefGoogle Scholar
(3)Mikhlin, S. G.Integral equations (Second Revised Edition) (Macmifian, New York, 1964).Google Scholar
(4)Buckholtz, J. D.Power series whose sections have zeros of large modulus. Trans. Amer. Math. Soc. 117 (1965), 157–166.CrossRefGoogle Scholar
(5)Tsuji, M.On the distribution of the zero points of sections of a power series. J. Math. Soc. Japan, 1 (1924), 109–140.CrossRefGoogle Scholar
(6)Lalesco, T.Sur la fonction D(λ) do Fredhoim. C. R. Acad. Sci. Paris 145 (1907), 1136–1137.Google Scholar
(7)Goursat, E.A course in mathematical analysis, vol. III, Part Two, 104–105 (Dover, New York, 1964).Google Scholar
(8)Copson, E. T.An introduction to the theory of functions of a complex variable, 121. (Corrected Edition) (Oxford, 1955).Google Scholar
(9)Hall, H. S. and Knight, S. R.Higher algebra (Fourth Corrected Edition), 267–272. (MacMillan, London, 1957).Google Scholar
(10)Swann, D. W. Some new classes of kernels whose Fredhoim determinants have order less than one (to appear in Trans. Amer. Math. Soc.).Google Scholar